Solveeit Logo
Login

Question

Question: The displacement of the particle in 0 to 3 s...

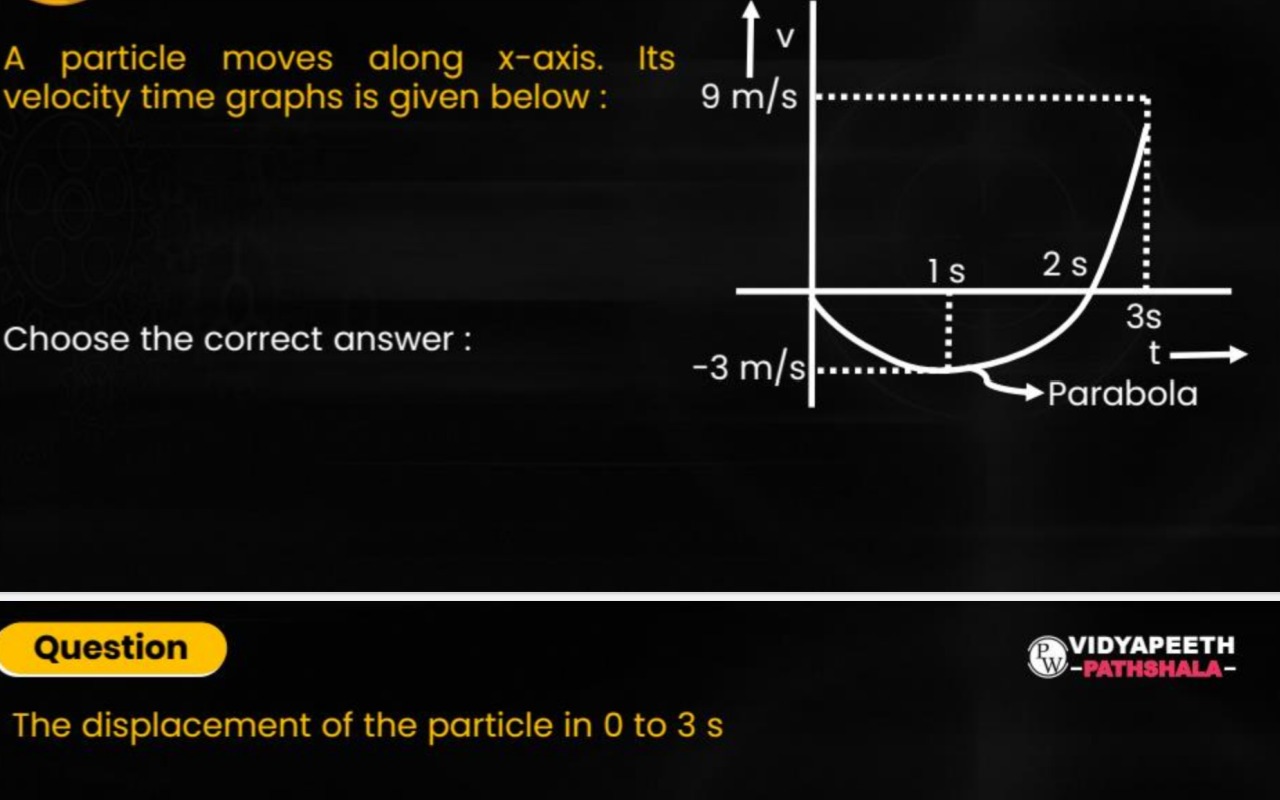
The displacement of the particle in 0 to 3 s

Answer

-2.25 m

Explanation

Solution

To find the displacement of the particle from 0 to 3 seconds, we need to calculate the area under the velocity-time (v-t) graph within this time interval. The graph is a parabola, so we first need to determine its equation.

1. Determine the equation of the parabola: The general equation of a parabola is v(t)=At2+Bt+Cv(t) = At^2 + Bt + C. From the given graph, we can identify three key points:

  • At t=0t = 0 s, v=−3v = -3 m/s.
  • At t=2t = 2 s, v=0v = 0 m/s (the graph crosses the t-axis).
  • At t=3t = 3 s, v=9v = 9 m/s.

Let's use these points to find the constants A, B, and C:

  • Using point (0, -3): −3=A(0)2+B(0)+C  ⟹  C=−3-3 = A(0)^2 + B(0) + C \implies C = -3

  • So, the equation becomes v(t)=At2+Bt−3v(t) = At^2 + Bt - 3.

  • Using point (2, 0): 0=A(2)2+B(2)−30 = A(2)^2 + B(2) - 3 0=4A+2B−3  ⟹  4A+2B=30 = 4A + 2B - 3 \implies 4A + 2B = 3 (Equation 1)

  • Using point (3, 9): 9=A(3)2+B(3)−39 = A(3)^2 + B(3) - 3 9=9A+3B−39 = 9A + 3B - 3 12=9A+3B  ⟹  4=3A+B12 = 9A + 3B \implies 4 = 3A + B (Dividing by 3) (Equation 2)

Now we solve the system of linear equations for A and B: From Equation 2, B=4−3AB = 4 - 3A. Substitute this into Equation 1: 4A+2(4−3A)=34A + 2(4 - 3A) = 3 4A+8−6A=34A + 8 - 6A = 3 −2A=3−8-2A = 3 - 8 −2A=−5-2A = -5 A=−5−2=2.5A = \frac{-5}{-2} = 2.5

Now substitute the value of A back into the expression for B: B=4−3(2.5)B = 4 - 3(2.5) B=4−7.5B = 4 - 7.5 B=−3.5B = -3.5

So, the velocity function is: v(t)=2.5t2−3.5t−3v(t) = 2.5t^2 - 3.5t - 3

2. Calculate the displacement: Displacement (Δx\Delta x) is the definite integral of velocity with respect to time over the given interval: Δx=∫t1t2v(t)dt\Delta x = \int_{t_1}^{t_2} v(t) dt

In this case, t1=0t_1 = 0 s and t2=3t_2 = 3 s. Δx=∫03(2.5t2−3.5t−3)dt\Delta x = \int_{0}^{3} (2.5t^2 - 3.5t - 3) dt

Integrate term by term: Δx=[2.5t33−3.5t22−3t]03\Delta x = \left[ \frac{2.5t^3}{3} - \frac{3.5t^2}{2} - 3t \right]_{0}^{3}

Now, evaluate the definite integral: Δx=(2.5(3)33−3.5(3)22−3(3))−(2.5(0)33−3.5(0)22−3(0))\Delta x = \left( \frac{2.5(3)^3}{3} - \frac{3.5(3)^2}{2} - 3(3) \right) - \left( \frac{2.5(0)^3}{3} - \frac{3.5(0)^2}{2} - 3(0) \right) Δx=(2.5×273−3.5×92−9)−(0)\Delta x = \left( \frac{2.5 \times 27}{3} - \frac{3.5 \times 9}{2} - 9 \right) - (0) Δx=(2.5×9−31.52−9)\Delta x = \left( 2.5 \times 9 - \frac{31.5}{2} - 9 \right) Δx=(22.5−15.75−9)\Delta x = \left( 22.5 - 15.75 - 9 \right) Δx=22.5−24.75\Delta x = 22.5 - 24.75 Δx=−2.25\Delta x = -2.25 m

The displacement of the particle in 0 to 3 s is -2.25 m.