Question

A particle moves along a circular path with decreasing speed. Then
A. its angular momentum remains constant
B. its resultant acceleration is towards the centre
C. particle moves in a spiral path with decreasing radius
D. the direction of angular momentum remains constant

Answer 1

We will look at the options provided and take a look at the angular momentum, acceleration, path and radius of the given particle undergoing a decrease in speed. Then we will try to determine if they follow the same trend as in the options provided.

Complete step by step answer:
First, we will check for the angular momentum of the body. Angular momentum is defined as the product of the moment of inertia and angular velocity. So angular momentum can be written as $L=I\omega =m{{r}^{2}}\dfrac{v}{r}=mvr$. Here we are given that the magnitude of v reduces, then the angular momentum must also reduce. Hence, the first option is not correct.
Next, we will check for the resultant acceleration. The particle will have two accelerations, centripetal acceleration which keeps the particle moving in a circle and is towards the centre of the circle made by the motion of the particle and tangential acceleration which reduces the speed of the particle and will be perpendicular to centripetal acceleration, their sum will not be acting towards the centre. Hence, option B is also not correct.

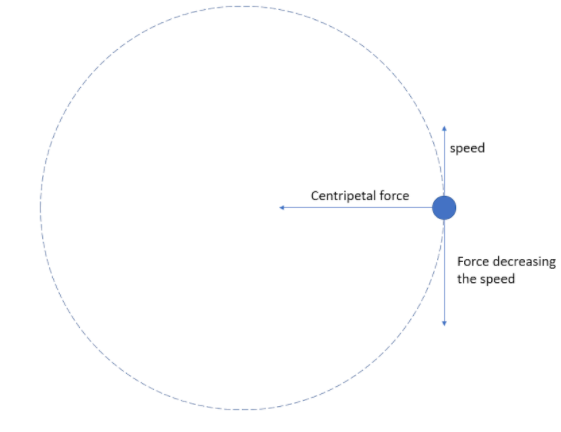
It is only given that the speed reduces, and we are not given that the centripetal acceleration remains constant. So, the radius of the motion must not change and remain constant. Option C will also not be correct.
The angular momentum as we saw changes in magnitude, but its direction will change if the directions of angular velocity changes. But as that does not happen, the direction of angular momentum will remain constant. Hence the correct option is D, i.e. the direction of angular momentum remains constant.

Note:
If we were given that the particle was moving with a constant velocity or angular momentum, then its radius will also change but as that is not the case here, we will not assume that. Also, as it is only given that speed reduces, we have considered that it does not go in a negative direction, if that happens the direction of angular momentum must change.