Question

A particle moves 12 m towards East then moves 5 m towards North and moves vertically 6 m. Find the displacement.

Answer 1

We can draw Cartesian components in three dimensions and we can observe that we are just given the x, y and z components of the vector and with the help of simple vector algebra we can determine the displacement.
Formula used:
The magnitude of a position vector is written as:
$r = \sqrt{x^2 + y^2 + z^2 }$
where x, y and z are the components of that position vector along the three directions respectively.

Complete answer:
We are given that the particle moves 12 m towards east this means that it has travelled 12 m along the x axis. If we consider our starting point to be the origin, then x = 12 m is the information we have till now. Then it is given that the particle moves 5 m towards the north which means that it moves along the y axis giving us y = 5 m. Finally, the particle moves 6 m vertically giving us z = 6 m. Here, a rough sketch for the motion of the particle has been provided.

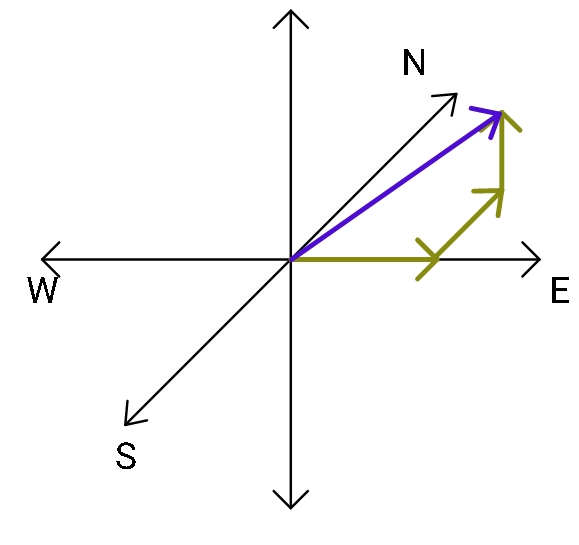
We have the three components of our position vector, with magnitude written as:
$r = \sqrt{12^2 + 5^2 + 6^2 } = \sqrt{205}$ = 14.317 m.
Therefore, the displacement of the particle from the origin is going to be equal to the magnitude of the position vector that we have calculated here which is 14.3 m approximately.

Note:
There is a fundamental difference between the terms distance and displacement. Calculating displacement means finding the shortest distance between a particle's final and initial positions. If we were asked how much distance the particle travelled in its path, we would have calculated 12 + 5 + 6 = 23 m.