Question

A particle located at $x = 0$ and time $t = 0$ starts moving along the positive x−direction with a velocity $v$ that varies as $v = \alpha \sqrt x$. Where $a$ is a constant. Then The displacement of the particle at time t:
A) ${\alpha ^2}{t^2}$
B) $\dfrac{{{\alpha ^2}{t^2}}}{2}$
C) $\dfrac{{{\alpha ^2}{t^2}}}{4}$
D) None

Answer 1

Displacement can be obtained by the differentiation of velocity.we will equate the velocity with the displacement and integrating the equation at x = 0 and t = 0.

Formula used:
$v = \dfrac{{ds}}{{dt}}$

Complete step by step answer:

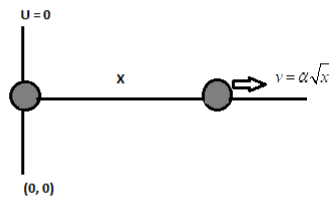
As per the question we have,
$v = \alpha \sqrt x$
$v = \dfrac{{ds}}{{dt}}$
$\dfrac{{ds}}{{dt}} = \alpha \sqrt x$
$\dfrac{{ds}}{{\sqrt x }} = \alpha \;dt$
Integrating on both sides we have,
\mathop \smallint \nolimits_0^x \dfrac{{ds}}{{\sqrt x }} = \mathop \smallint \nolimits_0^t \alpha \;dt
$\left( {2\sqrt x } \right)_0^x = \alpha \left( t \right)_0^t$
$2\sqrt x = \alpha t \Rightarrow \sqrt x = \dfrac{{\alpha t}}{2}$
By squaring on both sides we have,
$x = \dfrac{{{\alpha ^2}{t^2}}}{4}$

Additional information:
The by-product of a function representing the position of a particle on a line at a time is the instantaneous velocity. The by-product of the velocity, which is the second by-product of the position function, represents the acceleration of the particle at the time $t$
A positive velocity shows that the position is increasing as time increases, whereas a negative velocity indicates that the position is decreasing with respect to time. If the distance remains constant, then the velocity will be zero.
The average velocity between two points on the path in the limit that the time between the two points approaches zero.

Note: A positive acceleration shows that the velocity is increasing with respect to time, and the negative acceleration implies that the velocity is decreasing with respect to time.
If the velocity remains constant at an interval of time, then the acceleration will be zero in the interval.