Question

A particle is thrown vertically upwards with a velocity $11.2\text{ km}{{\text{s}}^{\text{-1}}}$ from the surface of earth. Calculate the velocity at height 3R, where R is the radius of the earth.
$\begin{aligned} & A)\simeq 9.25\text{ km}{{\text{s}}^{\text{-1}}} \\\ & B)\simeq 5.6\text{ km}{{\text{s}}^{\text{-1}}} \\\ & C)\simeq 11.2\text{ km}{{\text{s}}^{\text{-1}}} \\\ & D)\simeq 4.3\text{ km}{{\text{s}}^{\text{-1}}} \\\ \end{aligned}$

Answer 1

We will use the law of conservation of energy to solve this question. That means, the sum of kinetic energy of the particle and gravitational potential energy at distance R will be equal to the sum of kinetic energy of the particle and gravitational potential energy at 3R will be equal. By equating this expression, we can find the velocity of a particle at 3R.
Formula used:
$\begin{aligned} & K.E=\dfrac{1}{2}m{{v}^{2}} \\\ & {{U}_{(r)}}=-\dfrac{GMm}{r} \\\ \end{aligned}$

Complete answer:
Let us consider a particle of mass m thrown vertically upwards with velocity v. Let its velocity be v’ at the height 3R from the surface of earth.

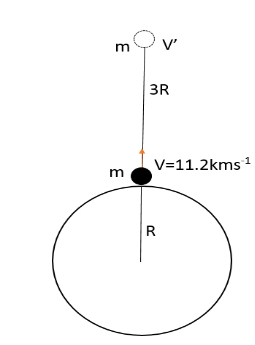
According to the law of conservation of energy, total energy will be conserved. That means, net energy at R and 3R will be equal. Total energy of the particle will be sum kinetic energy and gravitational potential energy.
Total energy of the particle at R will be given by,
$\begin{aligned} & T.E=K.E+{{U}_{\left( r \right)}} \\\ & \Rightarrow T.E=\dfrac{1}{2}m{{v}^{2}}-\dfrac{GMm}{r} \\\ \end{aligned}$
Where, m is the mass of the particle.
v is the velocity of a particle at R.
G is a universal gravitational constant.
M is the mass of the earth.
r is the distance between two centres of masses of the bodies.
Therefore, total energy of the particle at R will be,
$T.E=\dfrac{1}{2}m{{v}^{2}}-\dfrac{GMm}{R}$ --- (1)
Therefore, total energy of the particle at 3R will be,
$T.E=\dfrac{1}{2}m{{\left( v' \right)}^{2}}-\dfrac{GMm}{\left( R+3R \right)}=\dfrac{1}{2}m{{\left( v' \right)}^{2}}-\dfrac{GMm}{4R}$ --- (2)
Where, v’ is the velocity of the particle at 3R.
Now, according to the law of conservation of energy, (1) = (2).

& \Rightarrow \dfrac{1}{2}m{{v}^{2}}-\dfrac{GMm}{R}=\dfrac{1}{2}m{{\left( v' \right)}^{2}}-\dfrac{GMm}{4R} \\\ & \text{multiplying the whole equation with 2,} \\\ & \Rightarrow {{v}^{2}}-\dfrac{2GM}{R}={{\left( v' \right)}^{2}}-\dfrac{2GM}{4R} \\\ & \Rightarrow {{v}^{2}}-{{\left( v' \right)}^{2}}=-\dfrac{2GM}{4R}+\dfrac{2GM}{R} \\\ & \Rightarrow {{v}^{2}}-{{\left( v' \right)}^{2}}=\dfrac{6GM}{4R} \\\ & \Rightarrow {{\left( v' \right)}^{2}}={{v}^{2}}-\dfrac{6GM}{4R} \\\ \end{aligned}$$ $$\begin{aligned} & \text{since }g=\dfrac{GM}{{{R}^{2}}}, \\\ & \Rightarrow {{\left( v' \right)}^{2}}={{v}^{2}}-\dfrac{3}{2}gR \\\ & \text{Where, g is acceleration due to gravity and R is the radius of earth}\text{.} \\\ & \Rightarrow v'=\sqrt{{{\left( 11.2 \right)}^{2}}-\dfrac{3}{2}gR}\text{ } \\\ & \text{since }g=9.8m/{{s}^{2}}=\dfrac{9.8}{1000}km/{{s}^{2}}\text{ and }R=6400km, \\\ & \Rightarrow v'=\sqrt{{{\left( 11.2 \right)}^{2}}-\dfrac{3}{2}\times \dfrac{9.8\times 6400}{1000}} \\\ & \Rightarrow v'=\sqrt{{{\left( 11.2 \right)}^{2}}-\left( 94.08 \right)}\simeq 5.6km{{s}^{-1}} \\\ \end{aligned}$$ **So, the correct answer is “Option B”.** **Note:** While solving this question, we must be aware of converting all the units into same as we done in case of acceleration due to gravity, where we changed $m/{{s}^{2}}$ into $km/{{s}^{2}}$. Not keeping a single unit for a certain parameter throughout the solution will lead to calculation error and hence to wrong answer.