Question
Question: A particle is released on a vertical smooth semicircular track from point X, so that OX makes an ang...
A particle is released on a vertical smooth semicircular track from point X, so that OX makes an angle, θ, from the vertical (see figure). The normal reaction of the track on the particle vanishes at point Y, where OY makes an angle ϕ with the horizontal. Then
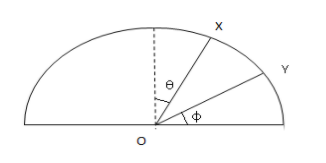
A. sinϕ=cosθ
B. sinϕ=21cosθ
C. sinϕ=32cosθ
D. sinϕ=43cosθ
Solution
Find the distance the particle travels when it falls from point X to point Y. Use work-energy theorem to find the energy of the particle when it falls. Check for all the forces acting on the particle at point Y.
Complete Step by step answer: Let R be the radius of the semicircle and h be the distance between point X and point Y
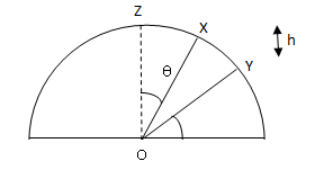
The component of OX along OZ is Rcosθ and component of OY along OZ is Rsinϕ
Therefore, the distance travelled by the particle when it is released from X to Y is
h=Rcosθ−Rsinϕ
Now, due to work done by gravity when the particle falls, it gains a velocity. Let v be the velocity of the particle. From work-energy theorem we have,
Work done by gravity = gain in kinetic energy of the particle
⇒mgh=21mv2
Where mgh is the work done by the gravity and 21mv2 is the kinetic energy of the particle.
⇒v=2gh
Substituting the value of h we get,
v=2g(Rcosθ−Rsinϕ)
Now, we draw a free body diagram, showing all the forces acting on the particle
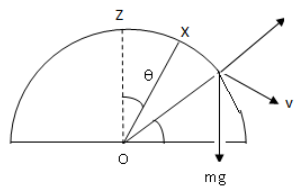
At point Y, we have along radial direction in circular motion ( in frame of particle)
N+Rmv2=mgsinϕ (i)
Where N is the normal reaction and ϕ is the angle between force mg and velocity v
Given, the normal reaction vanishes, N=0
Therefore, equation (i) becomes,
Rmv2=mgsinϕ (ii)
Putting the value of v in equation (ii), we get
