Question
Question: A particle is released at point P(-3,3) on a smooth vertical parabolic track \(y=\dfrac{{{x}^{2}}}{2...
A particle is released at point P(-3,3) on a smooth vertical parabolic track y=2x2. It slides down the track and leaves the contact with the track at a point Q(1,1) and again touches the horizontal track at a point R as shown in figure. Distance QR equals (Take g=10ms−2 and x and y in meter)
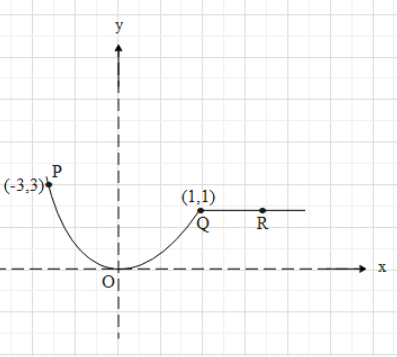
Solution
First calculate the total work done on the particle by the gravitational force. Then use the work-energy theorem that says that the total work done on a particle is equal to the change in its kinetic energy. With this, calculate the speed of the particle at point Q. Then find the angle of projection at point Q by finding the slope of the tangent to the parabola at Q. Later, use the formula for the range of a projectile.
Formula used:
W=mgh
K=21mv2
R=gu2sin2θ
Complete answer:
We know that the earth exerts a gravitational force on a body. The gravitational force on a body is always directed downwards in the vertical direction.
Therefore, when the particle is released from given the point, it will accelerate downwards along the surface of the track under the force of gravity.
This means that the gravitational force will do a positive work on the particle and when the particle rises from the bottom most point, the gravity will do a negative work.
The work done by gravitational force is given as W=mgh, where m is the mass of the particle, g is acceleration due to gravity and h is change in height of the particles (or we can also say the net vertical displacement).
In this case, h=3−1=2cm.
The total work done on a particle is equal to the change in its kinetic energy.
i.e. W=ΔK.
In this case, ΔK=21mv2, v is the speed of the particle at point Q.
Therefore, we get that
mgh=21mv2
⇒v2=2gh.
Substitute the values of g and h.
⇒v2=2(10)(2)=40
⇒v=40=210ms−1.
After the particle leaves the contact at point Q, it undergoes a projectile motion. Therefore, the length QR is the range of the projectile.
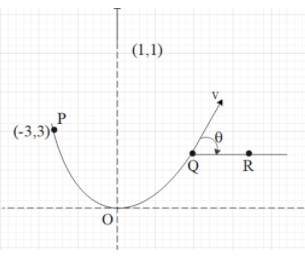
The range of the projectile is given as R=gu2sin2θ ….. (i), where u is the initial speed of the projectile and θ is the angle of projection.
In this case, u=v=210ms−1.
Let us find the value of θ.
In this case, θ is also the angle that the tangent to the parabolic track at point Q. The slope of the tangent is given as tanθ=dxdy.
Let us find the slope of tangent at point Q. Consider the given equation of the parabolic path.
i.e. y=2x2.
Differentiate the equation wrt x.
⇒dxdy=22x=x.
At point Q, x=1.
⇒dxdy=1
⇒tanθ=dxdy=1
⇒θ=tan−11=45∘.
Substitute the values of θ, u and g in (i).
⇒R=10(210)2sin2(45∘)=1040sin(90∘)=1040=4m
(Note that sin(90∘)=1).
This means that the length of QR is 4m.
Note:
We can also find the speed of the particle at point Q with the law of conservation of energy. According to the law of conservation of the energy, the sum of the potential energy and the kinetic energy of the particle is conserved.
This means that the sum of potential energy and kinetic energy at point P is equal to the sum of the potential energy and the kinetic energy at point Q.
The potential energy at height h is given as U = mgh.
