Question

A particle is projected with an angle of projection θ to the horizontal line passing through the points (P,Q) and (Q,P) referred to horizontal and vertical axes (can be treated as x-axis and y-axis respectively).
The angle of projection can be given by
A. ${\tan ^{ - 1}}\left[ {\dfrac{{{P^2} + PQ + {Q^2}}}{{PQ}}} \right]$
B. ${\tan ^{ - 1}}\left[ {\dfrac{{{P^2} - PQ + {Q^2}}}{{PQ}}} \right]$
C. ${\tan ^{ - 1}}\left[ {\dfrac{{{P^2} + {Q^2}}}{{2PQ}}} \right]$
D. ${\sin ^{ - 1}}\left[ {\dfrac{{{P^2} + PQ + {Q^2}}}{{PQ}}} \right]$

Answer 1

This is the case of projectile motion where the particle is projected with some angle to the horizontal. The acceleration acting on the projectile is only in vertical direction because gravity will be acting only in vertical direction and along horizontal direction there is no force.

Formula used:
$y = x\tan \theta \: - \:\dfrac{{g{x^2}}}{{2{u^2}{{(\cos \theta )}^2}}}$

Complete step by step answer:
When a particle is projected with some angle to the horizontal then that particle will have both horizontal displacement and vertical displacement. Since there will be no force along the horizontal direction the velocity along the horizontal direction will be the same throughout its motion while there is force along the vertical direction so velocity along vertical direction will vary.
Along the horizontal direction let the displacement be ‘x’ and initial velocity be ‘$u\cos \theta$’ and ‘t’ is time and acceleration is zero. Along the vertical direction let the displacement be ‘y’ and initial velocity be ‘$usin\theta$’ and ‘t’ is time and acceleration is $g$
Whereas theta is the angle of projection with horizontal and ‘u’ is the magnitude of initial velocity. It is denoted clearly in the below figure.

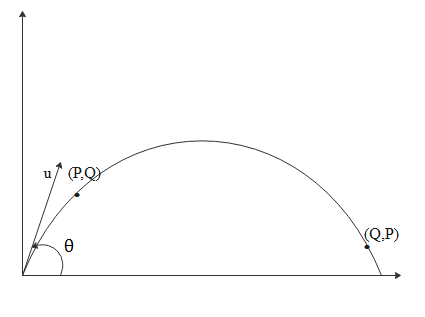
The equation of trajectory is given by
$y = x\tan \theta \: - \:\dfrac{{g{x^2}}}{{2{u^2}{{(\cos \theta )}^2}}}$
The particle passes through (P,Q) and (Q,P), hence we will have two equations by substituting these in the trajectory equation.
$y = x\tan \theta \: - \:\dfrac{{g{x^2}}}{{2{u^2}{{(\cos \theta )}^2}}}$
$P = Q\tan \theta \: - \:\dfrac{{g{Q^2}}}{{2{u^2}{{(\cos \theta )}^2}}}$ for the point (Q,P)
$Q = P\tan \theta \: - \:\dfrac{{g{P^2}}}{{2{u^2}{{(\cos \theta )}^2}}}$ for the point (P,Q)
In the above two equations the common term is $\dfrac{g}{{2{u^2}{{(\cos \theta )}^2}}}$. So by eliminating that common term we will get
$\theta \: = {\tan ^{ - 1}}\dfrac{{[{P^2} + {Q^2} + PQ]}}{{[PQ]}}$

So, the correct answer is “Option A”.

Note:
The formula which we have is applicable only if the acceleration due to gravity is constant and not varying. We can find the trajectory by finding the range and the angle of projection with the horizontal because the equation of trajectory we have can be written in terms of range too.