Question

A particle is projected with a velocity u making an angle $\theta$ with the horizontal. At any instant, its velocity v is at right angles to its initial u; then v is:
A).$u\; cos\theta$
B). $u\; tan\theta$
C). $u\; cot\theta$
D). $u\; sec\theta$

Answer 1

Try to gauge the type of motion that the particle undergoes and the trajectory it takes. In other words, since the particle is launched with a certain velocity at an angle, and is allowed to fall freely under gravity, this would be a case of projectile motion. Now, a good way to proceed from here would be to resolve $\vec{u}$ and $\vec{v}$ into their respective x and y-axis components and deduce which vector components are equivalent, following which the value of $v$ can be determined trigonometrically.

Complete step-by-step solution:
Let us try and illustrate the trajectory of the particle.
We have a particle that is launched with a velocity $u$ at an angle $\theta$. It freely falls under the action of gravity and flows a curved path. Such an object is called the projectile and such a motion is called projectile motion.
We are given that at some point in the trajectory the velocity is $v$ and at this point, the $\vec{v}$ vector points in a direction that is perpendicular to the $\vec{u}$.
We are required to find the value of $v$ at this point:

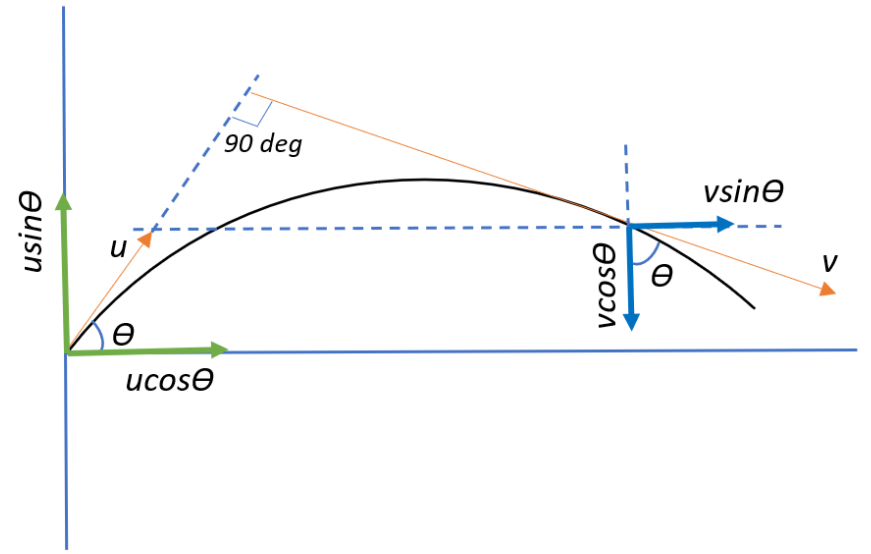
We begin by resolving our initial and final velocities into their horizontal and vertical components. From the diagram, we see that the horizontal components of $\vec{u}$ and $\vec{v}$ must be equal since the only external force acting is the gravitational force in the vertical direction which means that velocity changes only in the vertical direction whereas the horizontal velocity remains the same, i.e.,
$v\;sin\theta = u\;cos\theta$
$\Rightarrow v = u\dfrac{cos\theta}{sin\theta}$
$\Rightarrow v = u\;cot\theta$
Therefore, at the point where $\vec{v}$ is perpendicular to $\vec{u}$, $v$ possesses a value of $u\;cot\theta$.

Therefore, the correct option would be C. $u\;\cot\theta$

Note: While resolving the vectors into their horizontal and vertical components, remember to assign the $sine$ and $cosine$ values correctly since it is a common misconception that the horizontal side is the $cosine$ part and the vertical side is the $sine$ part.
The correct way to go about this would be to establish that the component that is adjacent to $\theta$ assumes a $cosine$ value, whereas the component that is opposite to $\theta$ assumes a $sine$ value.