Question

A particle is projected horizontally from height h. Taking g to be constant everywhere, kinetic energy E of the particle with respect to time t is correctly shown in (Neglected air resistance).
A)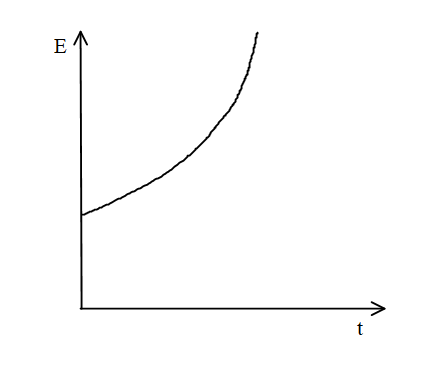
B)
C)
D)

Answer 1

Kinetic energy formula can be used to find the correct answer for this problem. Here the kinetic energy variation with time is asked so we need to see the variation of velocity with the time, the variation of initial velocity to final velocity with time can help us to calculate the correct answer for this problem.

Formula used: The kinetic energy for a particle of mass m and with a velocity v is given by$K.E = \dfrac{1}{2} \cdot m \cdot {v^2}$.

Complete step by step answer:
A particle is projected horizontally from height h. Taking g to be constant everywhere, kinetic energy E of the particle with respect to time t is correctly shown in (Neglected air resistance)
It is given in this problem that the particle is projected from a vertical height h horizontally, this means that the particle has some initial velocity and which means the particle has some initial kinetic energy and the Newton’s law motion has a relation which is $v = u + at$ and the acceleration is due to acceleration due to gravity therefore the relation becomes$v = u + gt$. Here we can see that the relation of the kinetic energy becomes,
For initial kinetic energy,
$K.E = \dfrac{1}{2} \cdot m \cdot {u^2}$
For final kinetic energy,
$K.E = \dfrac{1}{2} \cdot m \cdot {\left( v \right)^2} \\\ K.E = \dfrac{1}{2} \cdot m \cdot {\left( {u + gt} \right)^2} \\\ K.E = \dfrac{1}{2} \cdot m \cdot \left[ {{u^2} + {{\left( {gt} \right)}^2} + 2 \cdot u \cdot gt} \right] \\\$
For here we can see that the final kinetic energy of the particle is more than the initial kinetic energy so there is final kinetic energy which is more than the initial kinetic energy and also we can see that the relation is quadratic which means parabolic in nature open upwards.

Therefore the correct answer for this problem is option A.

Note: The students should not get confuse as the particle is projected horizontally and we have taken acceleration as g while applying the relation of Newton’s law of motion, so students here we can see that the particle is projected horizontally but the particle is not experiencing any acceleration in the horizontal direction which means that the acceleration due to gravity will be dominant and hence the acceleration should be taken acceleration due to gravity.