Question

A particle is projected from the ground with the speed $80m{s^{ - 1}}$ at an angle $30^\circ$ with the horizontal from the ground the magnitude of average velocity of the particle in the time interval t = 2 sec to t = 6 sec [ Take $g = 10m{s^{ - 2}}$
(A) $40\sqrt 3 m{s^{ - 1}}$
(B) $40m{s^{ - 1}}$
(C) $0m{s^{ - 1}}$
(D) $40\sqrt 2 m{s^{ - 1}}$

Answer 1

in order to solve the question, we will first use the formula of time of flight then we find the horizontal displacement using the formula of horizontal velocity of projectile motion at the point where particle is at same vertical height after then we will use the horizontal displacement to find the average velocity
Formula required to solve the question
$T = \dfrac{{2u\sin \theta }}{g}$
U is velocity
$g = 10m{s^{ - 2}}$
Horizontal Velocity of projectile motion = $u\cos \theta$
$horizontal{\text{ }}displacement = velocity \times time$
$average{\text{ }}velocity = \dfrac{{horizontal{\text{ }}displacement}}{{time}}$ .

Complete step by step answer:
In the question we are given a particle is projected from the ground and we have to find the magnitude of average velocity of the particle in the time interval t = 2 sec to t = 6 sec
A particle is projected from the ground with the speed = $80m{s^{ - 1}}$
Angle at which particle is projected = $30^\circ$
First of all, we will find the time of flight of the journey of particle by using the formula
$T = \dfrac{{2u\sin \theta }}{g}$
Now we will substitute the value of velocity (u) = $80m{s^{ - 1}}$ and value of theta = $30^\circ$
$T = \dfrac{{2 \times 80 \times \sin 30^\circ }}{{10}}\sec$
Value of $\sin 30^\circ = \dfrac{1}{2}$
Now we will equate the value of $\sin 30^\circ$ in the equation
$T = \dfrac{{2 \times 80 \times \dfrac{1}{2}}}{{10}}\sec$
Solving for time of flight
$T = 8\sec$
Now we will draw the diagram of particle using the time of flight at different time intervals such as 0 sec , 2 sec, 4 sec, 6 sec, 8 sec

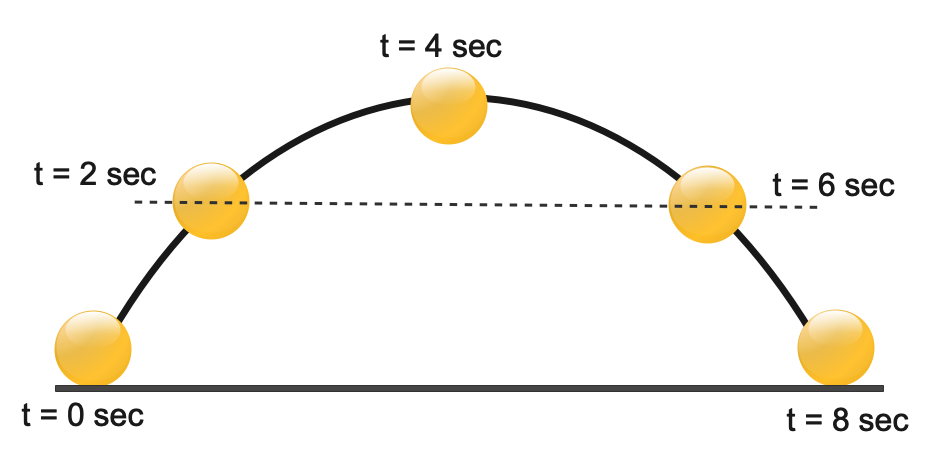
As we can see in the diagram that at t = 2 sec and t = 6 sec the height of the particle is same hence the vertical displacement is zero
Now we will find the horizontal displacement by using the formula of horizontal Velocity of projectile motion
Horizontal Velocity of projectile motion = $u\cos \theta$
Time taken = 6sec – 2 sec = 4 sec
Now we will use the formula of velocity, displacement and time to find the horizontal displacement
$horizontal{\text{ }}displacement = velocity \times time$
Substituting the value of Horizontal Velocity and time
$horizontal{\text{ }}displacement = u\cos \theta \times 4\sec$
Now we will substitute the value of velocity (u) = $80m{s^{ - 1}}$ and value of theta = $30^\circ$
$horizontal{\text{ }}displacement = 80\cos 30^\circ \times 4$
Value of $\cos 30^\circ = \dfrac{{\sqrt 3 }}{2}$
Now we will equate the value of $\cos 30^\circ$ in the equation
$horizontal{\text{ }}displacement = 80 \times \dfrac{{\sqrt 3 }}{2} \times 4$
$horizontal{\text{ }}displacement = 160\sqrt 3$
Now we will use the formula of average velocity to find it
$average{\text{ }}velocity = \dfrac{{horizontal{\text{ }}displacement}}{{time}}$
Substituting the value of horizontal displacement and time
$average{\text{ }}velocity = \dfrac{{160\sqrt 3 }}{4} = 40\sqrt 3 m{s^{ - 1}}$
Hence, the correct option is a) $40\sqrt 3 m{s^{ - 1}}$ .

Note:
Many of the people will make the mistake by not drawing the diagram as because it we can get the idea of particle at same height if we do not do that then we have to solve at both the direction horizontal and vertical so to nullify the vertical direction physical quantities we take their height same which it’s horizontal component same.