Question
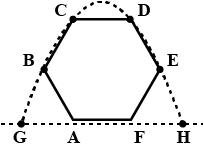
Question: A particle is projected from point G such that it touches the points B, C, D and E of a regular hexa...
A particle is projected from point G such that it touches the points B, C, D and E of a regular hexagon of side ‘a’. Its horizontal range GH is
A. 3a
B. 5a
C. 7a
D. None
Solution
Find the coordinates of the points B, C, D and E and put it in the equation of the parabolic path of the projectile described by the particle. The coordinates of the points B, C, D and E satisfy the equation of the parabola.
Complete step by step answer: Let origin be the midpoint of AF. Then the coordinates of B, C, D and E is given byB(−a,a23) , C(2−a,a3) , D(2a,a3) , E(a,a23)
The projectile will describe a parabola which is symmetrical about the y-axis. Lets the roots of the path traced by the parabola be r and –r. Then the equation of the parabola is given by y=k(x−r)(x+r) ⇒y=k(x2−r2)
Since the points B and C lie on this parabola, so its coordinates must satisfy the equation of the parabola. Putting the corresponding values of x and y of B iny=k(x2−r2), we get
a23=k(a2−r2) ………….(1)
Now, putting corresponding values of x and y of C iny=k(x2−r2), we get
a3=k(4a2−r2) ………….(2)
Dividing equations (1) and (2), we get
21=4(a2−4r2a2−r2) ⇒a2−4r2=8a2−8r2
⇒7a2=4r2 ⇒r=2a7
As the horizontal range is from –r to r, that is 2r.
So, the horizontal range is equal to 2×a7=7a
Hence, the correct option is (C).
Note: Projectile is the name given to a body thrown with some initial velocity with the horizontal direction and then allowed to move in two dimensions under the influence of gravity. The path followed by a projectile is called its trajectory. The path of a projectile projected horizontally from a point on the ground is a parabola which is symmetrical about the y-axis.
