Question
Question: A particle is projected at an angle 60 with speed \[10\sqrt{3}{m}/{s}\;\]from point A as shown in th...
A particle is projected at an angle 60 with speed 103m/sfrom point A as shown in the figure. At the same time, the wedge is made to move with speed 103m/stowards the right as shown in the figure. Then the time after which the particle will strike with the wedge is (g=10m/s2)
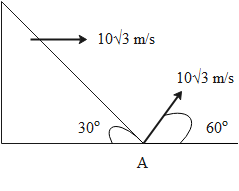
Solution
Firstly we will compute the velocities of the wedge and the particle separately, then, we will compute the velocity of the particle concerning the wedge. Using these velocity values we will compute the angles. Finally, we will use the standard formula to compute the time taken.
Formula used:
T=gcosβ2usin(α−β)
Complete step-by-step solution:
Firstly we will compute the velocity of the wedge concerning the axis.
The velocity of the wedge along the x-axis is,
Vwx=103m/s
The velocity of the wedge along the y-axis is,
Vwy=0m/s
Therefore, the velocity of the wedge is, Vw=103i.
Now, we will compute the velocity of the particle concerning the axis.
The velocity of the particle along the x-axis is,
