Question

A particle is projected along the inner surface of a smooth vertical circle of radius $R$ , its velocity at the lowest point being $\dfrac{1}{5}\sqrt {95Rg}$ . It will leave the circle at an angular distance _________ from the highest point.
A) $37^\circ$
B) $53^\circ$
C) $60^\circ$
D) $30^\circ$

Answer 1

The forces acting on the particle once it gets projected along the above-mentioned smooth surface are the centrifugal force, the normal reaction force and the weight of the particle. However, once the particle leaves the track the normal force will be zero. All the forces in play are conservative and so the energy will remain constant at the starting point and at the leaving point along the track.

Formulas used:
-The kinetic energy of a particle is given by, $K = \dfrac{1}{2}m{v^2}$ where $m$ is the mass of the particle and $v$ is its velocity.
-The potential energy of a particle is given by, $U = mgh$ where $m$ is the mass of the particle, $g$ is the acceleration due to gravity and $h$ is the height at which the particle is raised.
-The centrifugal force of a particle in a circular motion is given by, ${F_c} = \dfrac{{m{v^2}}}{r}$ where $m$ is the mass of the particle, $v$ is its velocity and $r$ is the radius of the circular path.

Complete step by step solution.
Step 1: Sketch a figure depicting the forces in play as the particle moves along the circle and list the given parameters of the problem.

In the above figure, point A represents the lowest point of the circle which is also the starting point of the particle. Point B represents the highest point of the circle and point P represents the point of exit of the particle.
At any point Q between A and P along the track, the forces acting on the particle are its weight $W = mg$ , the centrifugal force directed away from the centre ${F_c} = \dfrac{{m{v^2}}}{R}$ and the normal reaction force $N$ directed towards the centre as shown in the above figure.
As marked in the figure, we have to determine the angular distance $\theta$ from point B as the particle exits the track at point P.
The initial velocity of the particle or its velocity at A is given to be ${v_A} = \dfrac{1}{5}\sqrt {95Rg}$ .
Let $m$ be the mass of the particle and ${v_P}$ be the velocity of the particle as it leaves the track.
Step 2: Express the force balance equation for the particle at point P to obtain an expression for the velocity ${v_P}$ .
At point P, the particle leaves the track and so $N = 0$ . Then the forces in play are the weight of the particle and the centrifugal force. However, to write the force balance equation we consider the component of the weight $mg\cos \theta$ . This is shown in the figure below.

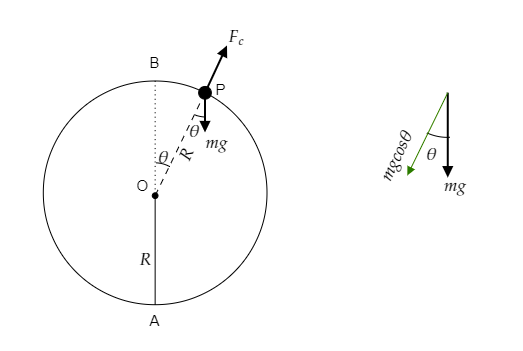
The force balance equation will then be $mg\cos \theta = \dfrac{{m{v_P}^2}}{R}$ .
$\Rightarrow {v_P} = \sqrt {Rg\cos \theta }$
Thus the velocity of the particle at point P is expressed as ${v_P} = \sqrt {Rg\cos \theta }$ .
Step 3: Apply the conservation of energy at point A and P to obtain the value of $\theta$ .
The energy of the particle at point A and at point P must be equal.
i.e., ${E_A} = {E_P}$ -------- (1)
At A, the total energy of the particle is ${E_A} = \dfrac{1}{2}m{v_A}^2$ ------- (2)
Consider the figure below.

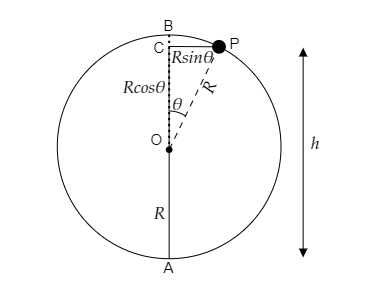
Here we resolve the radius into its components $OC = R\cos \theta$ and $CP = R\sin \theta$ . Also, we have $AO = R$ . Then at P, the height at which the particle is raised can be expressed as $h = R + R\cos \theta = R\left( {1 + \cos \theta } \right)$ .
At P, the total energy of the particle is ${E_P} = \dfrac{1}{2}m{v_P}^2 + mgR\left( {1 + \cos \theta } \right)$ ------- (3)
Substituting equations (2) and (3) in (1) we get, $\dfrac{1}{2}m{v_A}^2 = \dfrac{1}{2}m{v_P}^2 + mgR\left( {1 + \cos \theta } \right)$ -------- (4)
Now substituting for ${v_A} = \dfrac{1}{5}\sqrt {95Rg}$ and ${v_P} = \sqrt {Rg\cos \theta }$ in equation (4) we get, $\dfrac{1}{2}m{\left( {\dfrac{1}{5}\sqrt {95Rg} } \right)^2} = = \dfrac{1}{2}m{\left( {\sqrt {Rg\cos \theta } } \right)^2} + mgR\left( {1 + \cos \theta } \right)$
Cancelling out similar terms on either side we have $\dfrac{1}{2} \times \dfrac{{95}}{{25}} = \dfrac{1}{2} \times \cos \theta + \left( {1 + \cos \theta } \right)$
$\Rightarrow \dfrac{3}{2}\cos \theta = \dfrac{{19}}{{10}} - 1 = \dfrac{9}{{10}}$
$\Rightarrow \cos \theta = \dfrac{3}{5}$ or, we have $\theta = {\cos ^{ - 1}}\left( {\dfrac{3}{5}} \right) = 53 \cdot 13$
$\therefore$ the angular distance from the highest point is obtained to be $\theta = 53^\circ$ .
Hence the correct option is B.

Note: Here, the particle at the lowest point of the circular track (starting point) will possess only kinetic energy but at the leaving point P, the particle is raised to a height and hence will possess potential energy as well as kinetic energy. The surface is mentioned to be smooth so frictional forces which are non-conservative are absent and thus we say that the energy is conserved.