Question

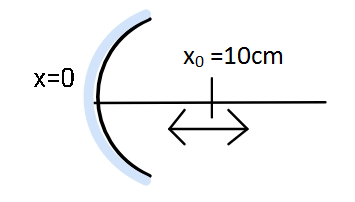
A particle is oscillating on the x-axis with an amplitude 2cm about the point $x_0 =10cm$ with a frequency $\omega$. A concave mirror of focal length 5cm is placed at the origin (see figure)
Identify the correct statements:
(A) The image executes periodic motion
(B) The image executes non-periodic motion
(C) The turning points of the image are asymmetric w.r.t. the image of the point at x=10cm
(D) The distance between the turning points of the oscillation of the image is $\dfrac{100}{21}$cm

A. (B), (D)
B. (B), (C)
C. (A), (C),(D)
D. (A), (D)

Answer 1

- Hint: Formula for spherical mirrors is to be used here for the analysis. The sign convention dictates that the distances measured along the direction of the ray are taken as positive and opposite to the ray are taken as negative.

Formula used:
For spherical mirror, focal length, object and image distance are related as:
$\dfrac{1}{f} = \dfrac{1}{u} +\dfrac{1}{v}$

Complete step-by-step solution
We simplify the formula for us first as we are asked about what happens with the image so:
$\dfrac{1}{v} = \dfrac{1}{f} - \dfrac{1}{u}$

For a concave mirror f is negative and u is negative. Given that u = -10cm and f= -5cm, we obtained:
$\dfrac{1}{v} = \dfrac{1}{-5 cm} - \dfrac{1}{-10 cm}$
Thus,
$v = \dfrac{10 \times -5}{10-5}$
v = -10cm. The image forms at the same point where the particle is. This happens when the particle is present at the centre of radius.
Therefore, statement (C) is correct.
Now, for the particle oscillating 2cm, we have 2 cases:
1. u= -12cm
Keeping this, we get:
$\dfrac{1}{v} = \dfrac{1}{-5 cm} - \dfrac{1}{-12 cm}$
$v= \dfrac{-60}{7}$cm
2. u= -8cm
$\dfrac{1}{v} = \dfrac{1}{-5 cm} - \dfrac{1}{-8 cm}$
$v= \dfrac{-40}{3}$cm
The difference between the two is:
$\dfrac{-40}{3} - \dfrac{-60}{7} = \dfrac{100}{21}$
So, (D) is correct.

Periodic motion can be checked by considering $u = 2\sin \omega t$
We might get
$v= \dfrac{10 \sin \omega t}{-\sin \omega t +5}$ sort of expression.
Here, the $\sin \omega t$ in the denominator has values between +1 and -1, so we are good to consider that the resultant image motion is periodic. So, statement (A) is okay too.
To conclude this, the correct answer is option C. (A), (C), (D) statements are correct.

Note: Sign convention should be handled carefully. In a hurry, one might replace u with -u then again keeps the value in negative form. This is susceptible to cause errors in the calculation. Also, remember the ray direction is positive sign direction. Distances are measured away from the mirror.