Question

A particle is moving with constant speed v on a circular path of r radius when it has moved by an angle of ${60^o}$ Find (i) Displacement of the particle (ii) Average velocity of the particle (iii) Average acceleration.

Answer 1

In order to solve this question, we will first draw the diagram to represent motion of the particle and then using the geometry of the circle we will solve for displacement, average velocity and average acceleration of the particle.

Complete step by step answer:
Let us draw the diagram in which OA and OB represent the radius r of the circular path followed by the particle and $\angle AOB = {60^o}$ Let AB represents displacement of the particle.

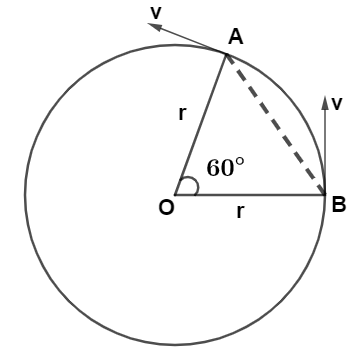
Now, In triangle OAB we see that
$OA = OB = r$ which shows that
$\angle OAB = \angle OBA$ by the property that angles opposite to equal sides of a triangle are equal.
So, we can write
$\angle OAB + \angle OBA + {60^o} = {180^o}$ sum of all angles of triangle OAB is ${180^o}$
$2\angle OAB = {120^o}$
$\Rightarrow \angle OAB = \angle OBA = {60^o}$ so,
triangle OAB is a equilateral triangle because all angles are equal of ${60^o}$ and since all sides of a equilateral triangle are also equal
$\Rightarrow OA = OB = r = AB$
$AB = r$
(i) Hence, the displacement of the particle AB is equal to the radius of the circular path r.
Now, Let ‘T’ be the time period of circular path which is written as
$T = \dfrac{{2\pi r}}{v}$ where v is the speed of the particle.
Now, in order to cover an angle of ${60^o}$ let ‘t’ be the time taken by particle so,
$t = \dfrac{T}{6}$ because six times the sixty degree of angle makes complete angle of ${360^o}$
$\Rightarrow t = \dfrac{{\pi r}}{{3v}}$
Now, average velocity is the ratio of displacement and time taken so,
${v_{average}} = \dfrac{{AB}}{t}$ where AB is the displacement so,
${v_{average}} = \dfrac{{3vr}}{{\pi r}}$
(ii) Hence, the average velocity of the particle is ${v_{average}} = \dfrac{{3v}}{\pi }$
Now, since the velocity of the particle is unchanged while going from Point B to point A and velocity of the particle is v and time is $t = \dfrac{{\pi r}}{{3v}}$ and average acceleration is simply the ratio of velocity and time taken so,
${a_{average}} = \dfrac{v}{t}$ on putting the values we get,
${a_{average}} = \dfrac{{3{v^2}}}{{\pi r}}$
(iii) Hence, the average acceleration of the particle is ${a_{average}} = \dfrac{{3{v^2}}}{{\pi r}}$

Note: It should be remembered that, here the asked displacement doesn’t mention about linear and angular because when a particle moves in circular orbit, particle also cover angular displacement here arc length of AB represents the angular displacement and calculated length of line AB is simply the linear displacement of the particle.