Question
Question: A particle is moving with constant speed in a circle as shown in fig. Find the angular velocity of t...
A particle is moving with constant speed in a circle as shown in fig. Find the angular velocity of the particle A with respect to fixed point B and C if angular velocity with respect to O is ω
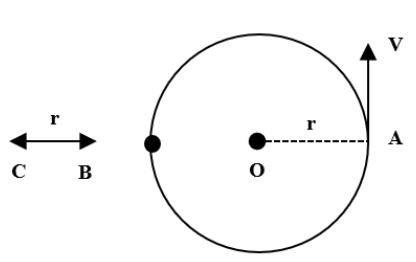
Solution
To solve this problem, use the relationship between angular velocity, linear velocity, and the distance of a particle from a fixed point. Using this relation find the angular velocity of particle A from point O. But the angular velocity of A with respect to O is given. So, substitute this value in the above-mentioned formula. Then, use the same formula to find the angular velocity of A with respect to B and C. Substitute the relation obtained from the angular velocity of A with respect to O. This will give the angular velocity of the particle A with respect to fixed point B and C.
Formula used:
ω=rv
Complete step by step solution:
Given:
Angular velocity of A with respect to O, ωAO=ω
Distance of point B from particle A rAB= 2r
Distance of point C from particle A rAC= 3r
Let the constant speed of the particle be v
Angular velocity is given by,
ω=rv
Where,
ω is the angular velocity
v is the linear velocity
r is the distance of the particle from a fixed point
Angular velocity of A with respect to O can be given by,
ωAO=rAOvAO …(1)
Substituting values in above equation we get,
ω=rv …(2)
Similarly, angular velocity of A with respect to B can be given by,
ωAB=rABvAB
Substituting values in above equation we get,
ωAB=2rv
Substituting equation. (2) in above equation we get,
ωAB=2ω
Similarly, angular velocity of A with respect to C can be given by,
ωAC=rACvAC
Substituting values in above equation we get,
ωAC=3rv
Substituting equation. (2) in above equation we get,
ωAC=3ω
Note: Angular velocity is analogous to linear velocity. Equation. (1) can also be written as, v=rω. From this equation, we can infer that the linear velocity is proportional to the distance from the center of rotation and linear velocity is directly proportional to the angular velocity. So, the greater the linear velocity, the greater is the angular velocity. Both linear and angular velocity have directions. Angular velocity has two directions with respect to the axis of rotation, either clockwise or anticlockwise. Whereas the linear velocity is tangent to the path.
