Question

A particle is moving with a velocity of $10m{\text{ }}{s^{ - 1}}$ towards east. After $10s$ its velocity changes to $10m{\text{ }}{s^{ - 1}}$ towards north. Its average acceleration is?
A. $0$
B. $\sqrt 2 m{\text{ }}{s^{ - 2}}$towards N-W
C. $\dfrac{1}{{\sqrt 2 }}m{\text{ }}{s^{ - 2}}$ towards N-E
D. $\dfrac{1}{{\sqrt 2 }}m{\text{ }}{s^{ - 2}}$ towards N-W

Answer 1

To solve this question, we will use the basic concept of average acceleration. First, we will draw the vectors along with the directions and by using the formula will find the average acceleration. And to find the direction we will use the parallelogram law in this way we will get our required solution.

Formula used:
$\vec a = \dfrac{{\Delta \vec v}}{{\Delta t}}$
Where,
$\vec a$ is the average acceleration,
$\Delta \vec v$ is the change in velocity and
$\Delta t$ is the total time interval.

Complete step by step answer:

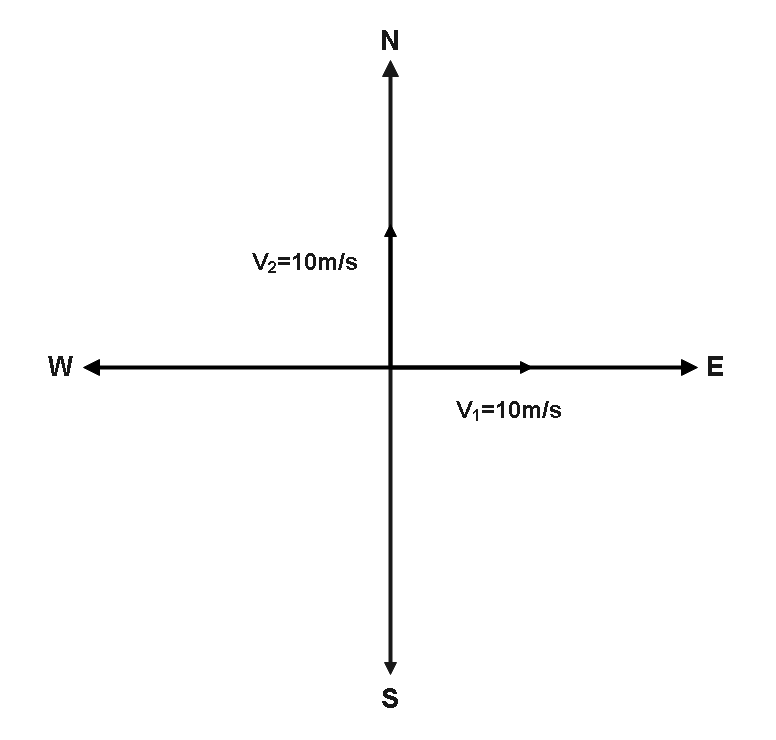
We can write the above-mentioned formula as,
$\vec a = \dfrac{{\Delta \vec v}}{{\Delta t}}$
$\Rightarrow \vec a = \dfrac{{{{\vec v}_2} - {{\vec v}_1}}}{{\Delta t}}$ -----(1)
So, now we will have to find the difference between${\vec v_2} - {\vec v_1}$ of the velocity vectors.
Or we can add both the vectors ${\vec v_2}$ and $- {\vec v_1}$ .
So, reversing the direction of the velocity vectors ${\vec v_1}$ to get,

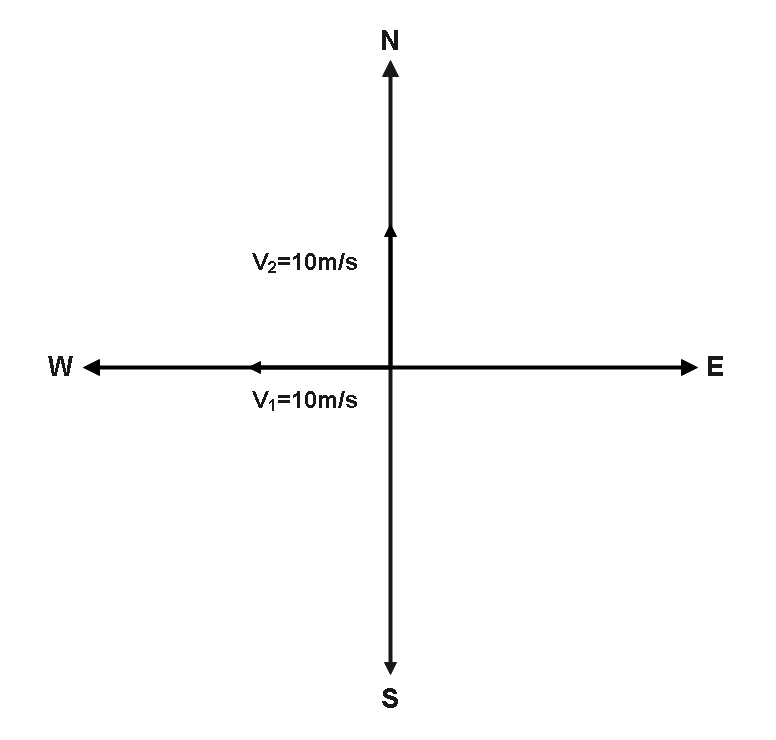
The consequent of these two vectors is now represented by the diagonal of the parallelogram created by these vectors, thanks to the diagonal law of vector addition. In the diagram below, the parallelogram and diagonal are depicted.

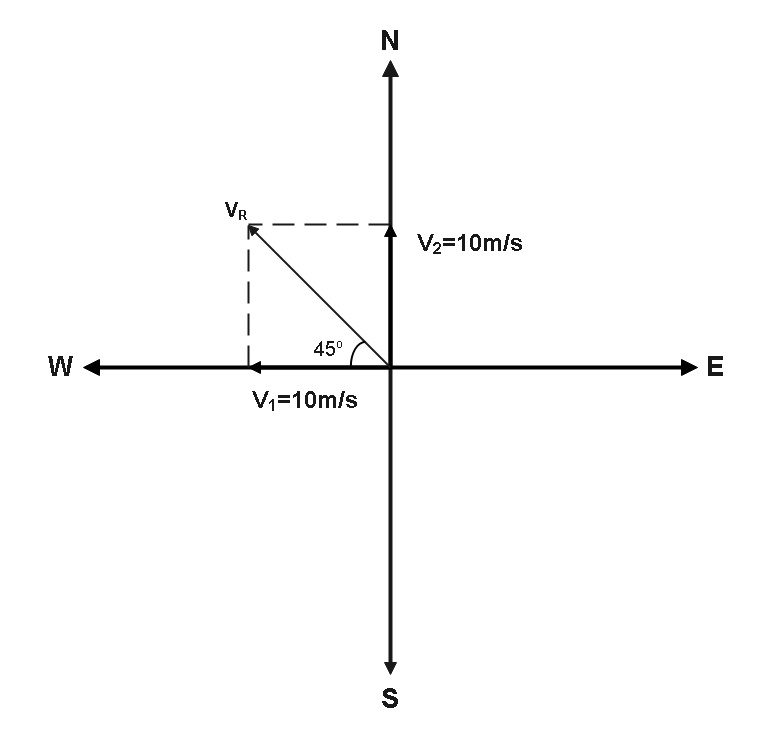
As in the above figure we can see that the diagonal is in the direction of north-west.
So the magnitude of the resultant will be,

$$\left| {{{\vec v}_R}} \right| = \sqrt {v_1^2 + v_2^2} \\\ \Rightarrow \left| {{{\vec v}_R}} \right| = \sqrt {{{10}^2} + {{10}^2}} \\\$$

$\Rightarrow \left| {{{\vec v}_R}} \right| = 10\sqrt 2 m{\text{ }}{s^{ - 1}}$ -----(2)
Now, from equation 1 we have,
$\Rightarrow \vec a = \dfrac{{{{\vec v}_2} - {{\vec v}_1}}}{{\Delta t}}$
Or we can say,
$\Rightarrow \vec a = \dfrac{{{{\vec v}_R}}}{{\Delta t}}$
If we write the above formula in terms of magnitude we will have,
$\left| {\vec a} \right| = \dfrac{{\left| {{{\vec v}_R}} \right|}}{{\Delta t}}$
And according to the question, it is given that $\Delta t = 10s$ so we can write,
$\left| {\vec a} \right| = \dfrac{{10\sqrt 2 }}{{10}} \\\ \left| {\vec a} \right| = \sqrt 2 m{\text{ }}{s^{ - 2}} \\\$
Now for direction, as the acceleration vector is parallel to the resultant vector ${\vec v_R}$ whose direction is north-west as seen above, so the direction of acceleration is also N-W.
Hence the correct option is B.

Note: Do not assume that the particle's acceleration is zero just because the initial and end magnitudes of the velocities are equal. Remember that because velocity is a vector quantity, the starting and end magnitudes of the velocity cannot be subtracted directly to get the acceleration.