Question
Question: A particle is moving on a circular path of radius R with uniform speed we. The magnitude of change i...
A particle is moving on a circular path of radius R with uniform speed we. The magnitude of change in velocity when the particle moves from P to Q is:- (∠PPOQ=40∘)
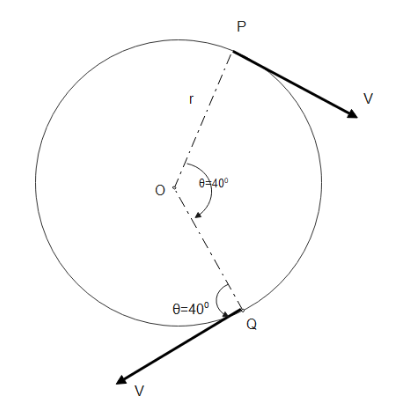
A. 2vcos 40∘
B. 2v sin 40∘
C. 2v sin 20∘
D. 2vcos 20∘
Solution
Read the question carefully and observe that here speed is given as constant, and it asks for the magnitude of the change in velocity, hence we must know the difference between speed and velocity as scalar and vectors. Also remember that speed remaining constant doesn’t mean there’s no acceleration.
Complete step by step answer:
Let us assume the velocity at the point P be V1. Now let us assume this point as the starting point and the other points are relative to it. We can consider the P point as either the Y axis or X axis. Let us consider it as the X axis here. Thus V1=Vi.
Now let the velocity at Q be V2 , it is at an angle 40∘ with the starting point P, thus it will have two components, one horizontal = Vcos40∘i and one vertical component = Vsin40∘j.
Now the change in velocity = ΔV=V2−V1=(Vcos40∘i−Vsin40∘j)−Vi
Thus the magnitude of this change is :
(Vcos40∘−V)2−(Vsin40∘)2
On solving the above expression we get the change of velocity = 2Vsin20∘.
Hence the answer is option B.
Note: It is very important to know the concept of vector units and scalar units to solve the problem. For instance, if the change in speed was asked, it would be zero as it is already that speed remains constant. Here velocity is always changing as there is change in direction continuously with the motion of the particle. Remember that this particle is able to change its direction continuously due to an acceleration towards the center of the circle, which is also varying the velocity.
