Question

A particle is moving on a circular path of 10 m radius. At any instant of time, its speed is ${\text{5m}}{{\text{s}}^{{\text{ - 1}}}}$ and the speed is increasing at a rate of ${\text{2m}}{{\text{s}}^{{\text{ - 2}}}}$. At this instant, the magnitude of the net acceleration will be nearly.
A. ${\text{3}}{\text{.2m}}{{\text{s}}^{{\text{ - 2}}}}$
B. ${\text{2m}}{{\text{s}}^{{\text{ - 2}}}}$
C. ${\text{2}}{\text{.5m}}{{\text{s}}^{{\text{ - 2}}}}$
D. ${\text{4}}{\text{.3m}}{{\text{s}}^{{\text{ - 2}}}}$

Answer 1

- Hint: In this problem you have to consider two accelerations translational and centripetal the resultant of that will be total acceleration. Doing this you will get the right answer.

Complete step-by-step solution :
The rough figure of the field can be drawn as:

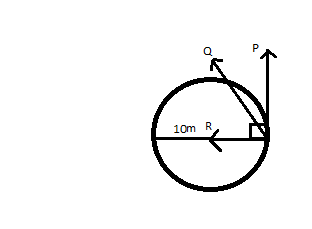
Here P is the linear acceleration ${{\text{a}}_l}$. R is the centripetal acceleration ${{\text{a}}_{\text{c}}}$.
We know that the rate of change of speed with respect to time is linear acceleration and it is given as ${{\text{a}}_l}{\text{ = 2m}}{{\text{s}}^{{\text{ - 2}}}}$ …….(1)
The speed of the particle is v = 5m/s.
The radius of the field is R = 10m.
We know that centripetal acceleration is ${{\text{a}}_{\text{c}}}{\text{ = }}\dfrac{{{{\text{v}}^{\text{2}}}}}{{\text{R}}}{\text{ = }}\dfrac{{{\text{5 x 5}}}}{{{\text{10}}}}{\text{ = 2}}{\text{.5m}}{{\text{s}}^{{\text{ - 2}}}}$ ………(2)
We also know that the angle between centripetal acceleration and linear acceleration in a circular path is 90 degrees.
And as the accelerations are vector quantity the resultant of all the accelerations is total acceleration ( ${{\text{a}}_{\text{t}}}$ ).
So, we do ${{\text{a}}_{\text{t}}}{\text{ = }}\sqrt {{{\text{a}}_{\text{l}}}^{\text{2}}{\text{ + }}{{\text{a}}_{\text{c}}}^{\text{2}}} {\text{ = }}\sqrt {{{{\text{(2}}{\text{.5)}}}^{\text{2}}}{\text{ + }}{{\text{2}}^{\text{2}}}} {\text{ = }}\sqrt {{\text{4 + 6}}{\text{.25}}} {\text{ = }}\sqrt {{\text{10}}{\text{.25}}} {\text{ = 3}}{\text{.2m}}{{\text{s}}^{{\text{ - 2}}}}$
So, the net acceleration is ${\text{3}}{\text{.2m}}{{\text{s}}^{{\text{ - 2}}}}$.
Hence, the correct option is A.

Note – To solve such questions of circular motions we need to always consider that there are two accelerations if speed is changing that is centripetal and translational both are at right angles to each other. If the speed is not changing then there is only centripetal acceleration in circular motion. The direction of centripetal acceleration is radially towards the centre of the circle. Knowing this will solve your problem and give the right answer.