Question

A particle is moving in a circular path of radius $a$ , with constant velocity $v$ as shown in figure. The centre of circle is marked by ‘C’ the angular momentum from the origin O can be written as:

(A) $va\left( {1 + \cos 2\theta } \right)$
(B) $va\left( {1 + \cos \theta } \right)$
(C) $va\cos 2\theta$
(D) $va$

Answer 1

A body experiencing circular motion would experience angular velocity $\omega$ but when linear velocity is considered in non-linear circumstances the perpendicular component of the linear velocity is taken. The non-perpendicular component of the velocity vector has no effect on the angular momentum of a body.
Formula used: We will be using the formula $L = m{v_ \bot }r$ where $L$ is the angular momentum of the body in circular motion, ${v_ \bot }$ is the perpendicular component of velocity vector, $r$ is the radius of the circular path in which the body was moving.

Complete step by Step answer:
We know that when a body is in circular motion it experiences angular velocity, which is given by $\omega$ and is related to linear velocity as ${v_ \bot } = \omega r$ . The linear velocity $v$ of the body is experienced due to centripetal force on the body and moves outward from the body, tangential to its circular path of motion.

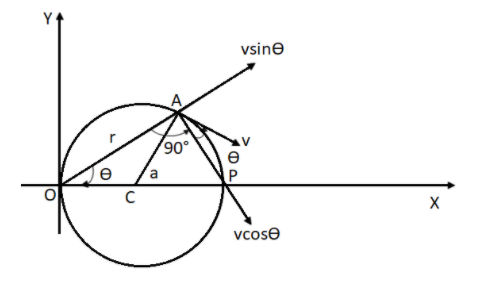
Let us make a construction and extend the line AP to touch the circle on its circumference, such that OP is the diameter. Now we know that by the property of a circle the angle subtended by the diameter on the circumference of the circle is a right angle, $\angle OAP = 90^\circ$ .
Also, by the property of the isosceles triangle the angles adjacent to the equal sides are equal thus, $\angle AOC = \angle CAO = \theta$. So, $\angle CAP$ will be $\left( {90^\circ - \theta } \right)$ . We know that the velocity vector caused by centripetal force will be perpendicular to the radius of the circle. Thus, the angle subtended by the line AC and velocity vector is $90^\circ$ . Thus, making the angle formed by velocity vector and the line AP,
$\angle A - \angle CAP = 90^\circ - \left( {90^\circ - \theta } \right) = \theta$ .
Now the velocity vector can be taken into 2 components: the vertical component along AP, $v\cos \theta$ and the horizontal component, $v\sin \theta$ . We know that the horizontal component of the velocity vector has no effect on angular momentum of the body.
Now in $\Delta OAP$ , $\cos \theta = \dfrac{{OA}}{{OP}}$ . OP is the diameter hence, $OP = 2a$ and let $OA = r$ .
$\cos \theta = \dfrac{r}{{2a}}$
$\Rightarrow r = 2a\cos \theta$
Now to find the angular momentum along the origin O,
$L = m{v_ \bot }r$
$\Rightarrow L = m \times v\cos \theta \times 2a\cos \theta$
[Since $v\sin \theta$ has no effect on the angular momentum along origin.]
$L = mva\left( {2{{\cos }^2}\theta } \right)$
According to the trigonometric formula, $2{\cos ^2}\theta = \left( {1 + \cos 2\theta } \right)$
$L = mva\left( {1 + \cos 2\theta } \right)$

Let us consider that the particle in motion has unit mass. Thus, the angular momentum of the particle along origin will be, $L = va\left( {1 + \cos 2\theta } \right)$ [option A]

Note: Centripetal force is the force that makes the body follow a curved path. The direction is always perpendicular to the direction of motion. This is why the horizontal component of velocity $v\sin \theta$ is neglected.