Question
Question: A particle is moving in a circle of radius r with a constant speed v. The change in velocity in movi...
A particle is moving in a circle of radius r with a constant speed v. The change in velocity in moving from P to Q is
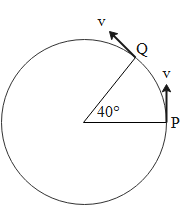
A. 2v cos 20∘ B. 2v sin 20∘ C. 2v cos 40∘ D. 2v sin 40∘
Solution
Hint: If we consider the particle to be moving in an x-y plane, then we can resolve the components of the velocity along the x-axis and y axis. Change in velocity is equal to difference between velocity at Q and the velocity at P.
Detailed step by step answer:
We are given a particle which is moving in a circle of radius r with a constant speed v. The diagram shows two points of the trajectory of the particle.
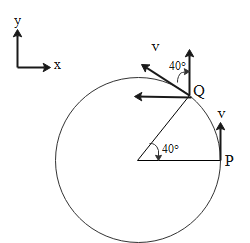
If we consider the particle is moving in a x-y plane then at point P, the expression for velocity can be written as follows since it's pointing towards the y-axis.
VP=Vj
For point Q, we must write the velocity vector in terms of its components as follows:
VQ=−Vsin40∘i+Vcos40∘j
Here the angle at Q has been calculated using the fact that a tangent to a circle subtends a right angle with the radius of the circle.
Now the change in velocity from P to Q can be given as
ΔV=VQ−VP =−Vsin40∘i+(Vcos40∘−V)j =−Vsin40∘i+V(cos40∘−1)j
Now we need to calculate the magnitude of this change in velocity which will give us the required answer.
\Delta V = |\overrightarrow {\Delta V} | = \sqrt {{{\left( { - V\sin 40^\circ } \right)}^2} + {{\left\\{ {V\left( {\cos 40^\circ - 1} \right)} \right\\}}^2}} \\\ = V\sqrt {{{\sin }^2}40^\circ + {{\left( {\cos 40^\circ - 1} \right)}^2}} \\\ = V\sqrt {{{\sin }^2}40^\circ + {{\cos }^2}40^\circ + 1 - 2\cos 40^\circ } \\\
Using the identity: sin2θ+cos2θ=1
ΔV=V2−2cos40∘ =V2(1−cos40∘)
Using the identity: 1−cosθ=sin22θ
ΔV=V4sin220∘ =2Vsin20∘
This is the required change in velocity; hence, the correct answer is option B.
Note: It is mentioned that the particle is moving with constant speed. It means that the magnitude of velocity is constant but when a particle moves in a circular orbit, its speed may remain constant but the direction of velocity changes at every point of the path. Velocity changes as it is a vector quantity and it is dependent on the direction of the vector.
