Question

A particle is moving in a circle of a radius $r$ with constant speed $v$ . The change in velocity in moving from P to Q is

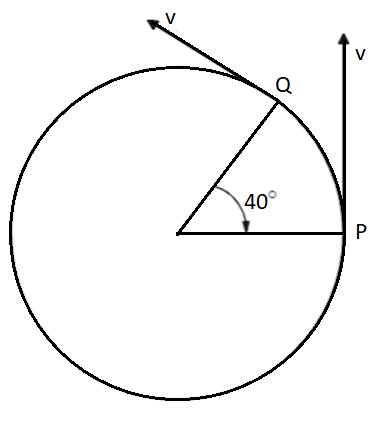
(A) $2v\cos 20^\circ$
(B) $2v\sin 20^\circ$
(C) $2v\cos 40^\circ$
(D) $2v\sin 40^\circ$

Answer 1

A resultant vector is the vector sum of the two vectors whose resultant is to be found. Since velocity is a vector quantity, it has both magnitude and direction. To find the change in velocity of the vectors we need to find the resultant vector and the angle between them. The resultant vector is given by, $\left| {\overrightarrow v } \right| = \sqrt {{{\left( {{v_i}} \right)}^2} + {{\left( {{v_f}} \right)}^2} - 2\left( {{v_i}} \right)\left( {{v_f}} \right)\cos \theta }$ .
Formula used: We will be using the formula to find the resultant velocity vector to find the change is velocity which is given by, $\left| {\overrightarrow v } \right| = \sqrt {{{\left( {{v_i}} \right)}^2} + {{\left( {{v_f}} \right)}^2} - 2\left( {{v_i}} \right)\left( {{v_f}} \right)\cos \theta }$ where $\left| {\overrightarrow v } \right|$ is the resultant velocity, ${v_i}$ is the initial velocity of the body, ${v_f}$ is the final velocity of the body and $\theta$ is the angle between the two velocity vectors ${v_i}$ and ${v_f}$ .

Complete step by step answer:
We know that the linear velocity of a body that executes circular motion is tangential to the motion and is perpendicular to the radius of the circular path. Thus, the linear velocity of the body at P, $v$ is perpendicular to the radius, $OP = r$ and the linear velocity of the body at Q, $v$ is perpendicular to the radius, $OQ = r$ .
We can also infer from the problem the body is moving from P to Q, thus making, ${v_i} = v = {v_f}$ . The initial and final velocities are the same in magnitude; however, they differ in directions which is why the resultant needs to be calculated by vector addition.

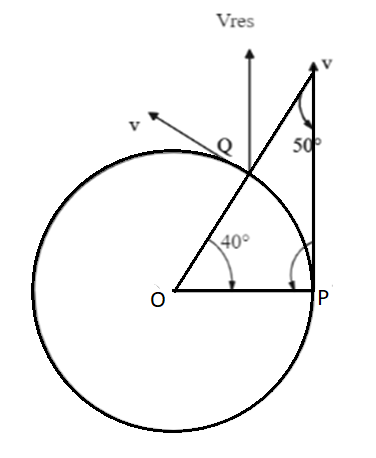
Let us make a few constructions and extend the radius OQ such that it makes an angle with the velocity vector from P. Since it makes a triangle the angle formed will be $50^\circ$. Now let us draw a resultant vector from Q . The angle subtended by the resultant velocity vector along the final velocity will be $40^\circ$ .
Applying the formula to find the resultant velocity,
$\left| {\overrightarrow v } \right| = \sqrt {{{\left( {{v_i}} \right)}^2} + {{\left( {{v_f}} \right)}^2} - 2\left( {{v_i}} \right)\left( {{v_f}} \right)\cos \theta }$
$\left| {\overrightarrow v } \right| = \sqrt {{{\left( v \right)}^2} + {{\left( v \right)}^2} - 2\left( v \right)\left( v \right)\cos \theta }$
$\left| {\overrightarrow v } \right| = \sqrt {2{v^2} - 2{v^2}\cos \theta }$
Taking common terms from the above equation we get,
$\left| {\overrightarrow v } \right| = \sqrt {2{v^2}(1 - \cos \theta )}$
We know that $\theta = 40^\circ$
$\left| {\overrightarrow v } \right| = \sqrt {2{v^2}(1 - \cos 40^\circ )}$
From the trigonometric formula, $1 - \cos 2\theta = 2{\sin ^2}\theta$
$\left| {\overrightarrow v } \right| = \sqrt {2{v^2}\left( {2{{\sin }^2}\left( {20^\circ } \right)} \right)}$
Solving the above equation, we get,
$\left| {\overrightarrow v } \right| = 2v\sin 20^\circ$
Thus, the resultant velocity of the above particle will be, $\left| {\overrightarrow v } \right| = 2v\sin 20^\circ$ .

Hence the correct answer is option B.

Note: We can also solve the above problem for resultant velocity using the parallelogram of vectors. From there we need to find the resultant angle between the two vectors more easily.