Question
Question: A particle is moving eastwards with velocity of 5 m/s. In 10 sec the velocity changes to 5 m/s north...
A particle is moving eastwards with velocity of 5 m/s. In 10 sec the velocity changes to 5 m/s northwards. The average acceleration in this time is
A
Zero
B
21m/s2toward north-west
C
21m/s2toward north-east
D
21m/s2toward north-west
Answer
21m/s2toward north-west
Explanation
Solution
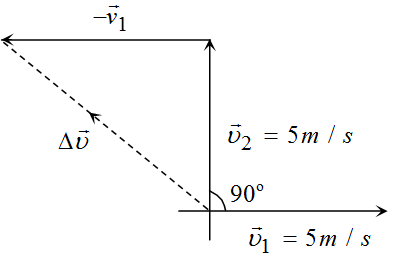
Δυ=υ2−υ1
Δυ=υ12+υ22−2υ1υ2cos90o=52+52=52Δυ=52
Average acceleration =ΔtΔυ=1052=21m/s2
toward north-west (As clear from the figure).