Question

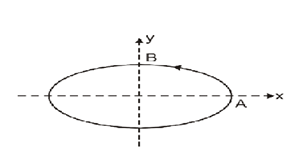
A particle is moving along an elliptical path with constant speed. As it moves from A to B, magnitude of its acceleration is:

A) Continuously increases.
B) Continuously decreases.
C) Remains constant.
D) First increases and then decreases.

Answer 1

As we know that If the particle is moving with a constant velocity or speed in an elliptical path, then the motion is said to be accelerated motion, so the direction of the velocity changes at every point of elliptical path.

Complete step by step answer:
Consider the question, we are given that a particle is moving along an elliptical path with a constant speed. And the particle moves from point $A$ to point $B$.
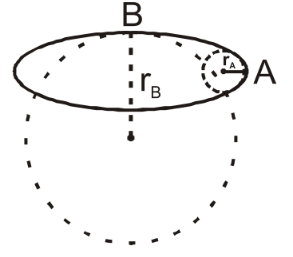
To understand the given information, when the particle is moving from $A$ to point $B$, we can observe from the figure$\left( 2 \right)$ that radius is increasing continuously.

We are given the constant speed, so, the speed on the tangent will be zero.
$\Rightarrow {a_t} = \dfrac{{dv}}{{dt}}$

Therefore, the tangential acceleration will be zero.
$\Rightarrow {a_t} = 0$

Now we will consider the radius of the curvature of the circle $R$, and the acceleration of the curvature is ${a_c}$ when the particle is moving towards the $B$ point.
$\Rightarrow {a_c} = \dfrac{{{v^2}}}{R}$
As the speed of the particle is constant, when the particle moves from A to B, the magnitude of its acceleration is decreasing because the radius of the curvature is increasing.
Therefore, when the particle is moving from A to B then the magnitude of its acceleration is continuously decreasing.

So, the option (B) is correct.

Note: In this question, as we know that the acceleration is the rate of change of the velocity. Here, the particle moves from point $A$ to point $B$, then the velocity or speed of the particle is constant. So, the acceleration of the particle will be zero.