Question

A particle is moving along a circular path with a constant speed of $10m{{s}^{-1}}$. What is the magnitude of change in velocity of the particle, when it moves through an angle of $60^\circ$ around the centre of the circle?
A. 0
B. $10m{{s}^{-1}}$
C. $10\sqrt{3}m{{s}^{-1}}$
D. $10\sqrt{2}m{{s}^{-1}}$

Answer 1

Hint: Here, the particle moves with a constant speed. Since it is moving in a circular path, the velocity will change its direction according to its position. So we have to do this problem by using vector algebra. The magnitude of change in velocity can find out from the magnitudes of initial and final velocities and their angle. Use vector rules to calculate the answer.

Formula used:
$|\Delta \vec{v}|=\sqrt{|{{{\vec{v}}}_{2}}{{|}^{2}}+|{{{\vec{v}}}_{1}}{{|}^{2}}-2|{{{\vec{v}}}_{1}}||{{{\vec{v}}}_{2}}|\cos \theta }$, where ${{\vec{v}}_{2}}$is the final velocity, ${{\vec{v}}_{1}}$ is the initial velocity and these vector velocities will make an angle $\theta$.

Complete step by step answer:

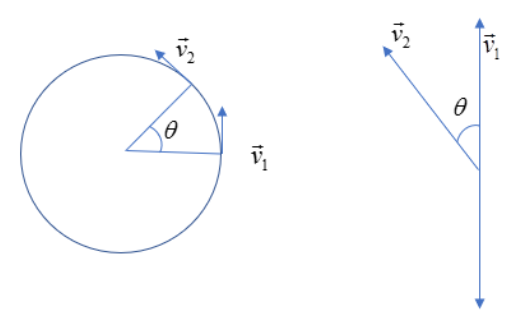
As we know the particle moves in a circular path with a constant speed of $10m{{s}^{-1}}$. Here, the velocity will change its direction even though the particle moves with the same magnitude of velocity. Therefore, the velocity vector is not constant in this case. So, we have to consider vector algebra to solve this problem since the velocity is a vector quantity.
As the particle moves in a uniform circular path, the velocity vector is always tangential to the circle, and at any time the angle between the tangents and the radii are the same. Here, we can take as final velocity vector as ${{\vec{v}}_{2}}$ and initial velocity vector as ${{\vec{v}}_{1}}$. These vector velocities will make an angle $\theta$. Here the angle is $60{}^\circ$. These vectors will arrange like as shown in the figure above. We can use $\Delta \vec{v}$ to represent the change in the velocity vector of the particle.
As we know, only the direction of velocity vectors is changing. So we can write as,
$|{{\vec{v}}_{1}}|=|{{\vec{v}}_{2}}|=v=10m{{s}^{-1}}$
Here the change in velocity vector will be,
$|\Delta \vec{v}|=|{{\vec{v}}_{2}}-{{\vec{v}}_{1}}|$
According to the vector rules,
$|\Delta \vec{v}|=\sqrt{|{{{\vec{v}}}_{2}}{{|}^{2}}+|{{{\vec{v}}}_{1}}{{|}^{2}}-2|{{{\vec{v}}}_{1}}||{{{\vec{v}}}_{2}}|\cos \theta }$
Since we are dealing magnitudes only, we alter this equation as,
$|\Delta \vec{v}|=\sqrt{{{v}^{2}}+{{v}^{2}}-2{{v}^{2}}\cos \theta }$
Now we can assign the given values to the equation.
$|\Delta \vec{v}|=\sqrt{{{10}^{2}}+{{10}^{2}}-2\times {{10}^{2}}\cos 60{}^\circ }$
$|\Delta \vec{v}|=10m{{s}^{-1}}$
Therefore, the correct answer is option B.

Note: We can do this problem in different ways. Since we are dealing with angles. However, the final answer will be the same. It is better to learn vector rules, to do problems easily. For multiple-choice questions like this, we can use a short cut to solve this problem in competitive exams. Because we have to save our time.
Change in velocity, $\Delta v=2v\sin \dfrac{\theta }{2}$
But this formula is not advised to do in the school exams.