Question

A particle is moving along a circular path of radius 5 m with a uniform speed $5m{s^{ - 1}}$. What will be the average acceleration when the particle completes half revolution?
A.${\text{ Zero}}$
B. ${\text{ 10}}m{s^{ - 2}}$
C. ${\text{ 10}}\pi {\text{ m}}{{\text{s}}^{ - 2}}$
D. ${\text{ }}\dfrac{{10}}{\pi }m{s^{ - 2}}$

Answer 1

Hint: For a particle moving in a circular path, the acceleration can be calculated by as the rate of change of velocity of object with time. The velocity is constant but its direction is changing with the motion of the particle which needs to be taken in account.

Formula used:
The formula for average acceleration is given as:
${a_{avg}} = \dfrac{{\Delta {\text{v}}}}{{\Delta t}}$
where $\Delta {\text{v }}$is the change in velocity and $\Delta t$ is the time taken.

Complete step-by-step answer:
We are given a particle which is moving along a circular path having a radius of 5m.
$\therefore r = 5m$
The particle is moving with a uniform velocity of 5m/s in the circular orbit.
$\therefore {\text{v}} = 5m/s$
We need to calculate the average acceleration when the particle completes its half trajectory. Diagrammatically, the situation can be represented as follows:

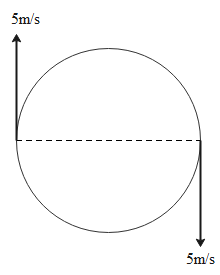
Velocity of the particle is constant but its direction must be taken into account. In the diagram, we can see that when a particle reaches its half trajectory, the final velocity is in the opposite direction to the initial velocity. Hence, the initial velocity and final velocity is given as:
${{\text{v}}_i} = 5m/s \\\ {{\text{v}}_f} = - 5m/s \\\$
Therefore, the overall change in velocity of the particle is given as
$\Delta {\text{v}} = {{\text{v}}_f} - {{\text{v}}_i} = 5 - \left( { - 5} \right) = 10m/s$
Now the time taken to complete half trajectory can be calculated as follows:
$\Delta t = \dfrac{{\pi r}}{{\text{v}}}$
Substituting the known values, we get
$\Delta t = \dfrac{{\pi \times 5}}{5} = \pi {\text{ s}}$
Now we can calculate the average acceleration by dividing change in velocity with the time taken as follows:
${a_{avg}} = \dfrac{{\Delta {\text{v}}}}{{\Delta t}} = \dfrac{{10}}{\pi }m/{s^2}$
Hence, the correct answer is option D.

Note: Though the magnitude of velocity is constant for the particle moving in circular orbit, the acceleration keeps changing at every point of the trajectory. The reason is that direction of velocity is changing at every point and since acceleration is a vector quantity, it depends on the direction of velocity as well as magnitude.