Question

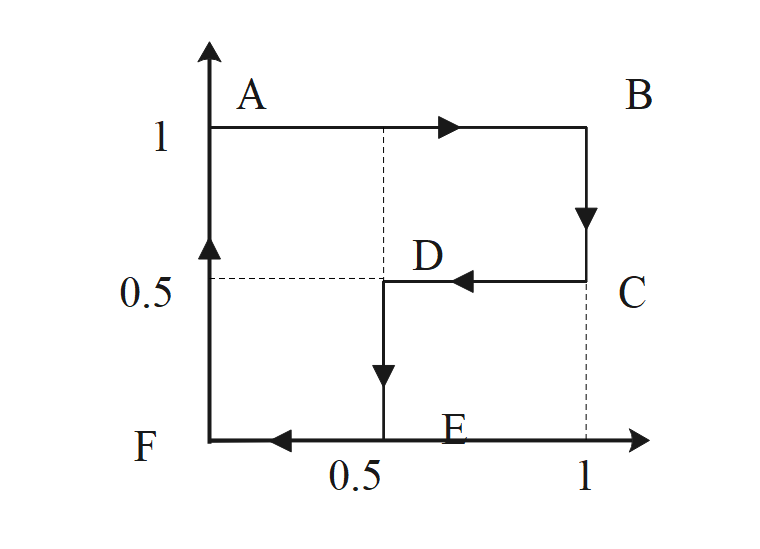
A particle is moved along a path AB−BC−CD−DE−EF−FA, as shown in figure in presence of a force $F=(\alpha yi+2\alpha xj)N$, where x and y are in meter and $\alpha =-1N{{m}^{-1}}$. The work done on the particle by this force F will be _______ joule.

Answer 1

As the work done is the product of force and the displacement. The force changes here as the particle moves from one place to another. Therefore, we need to apply integration for every turn or change in force. Hence, we can find the work done easily.

Complete step by step answer:
let us first write down the given values,
$F=(\alpha yi+2\alpha xj)N$
It is clear that the force changes as the particle travels from one place to another.
We need to calculate the force acting over each part of the total distance.
Let us first take a to b from x=0 to x=1, the y-coordinate is constant here. Therefore, the work done for this part of distance will be,
$\begin{aligned} & W=\int{\alpha ydx}=\alpha \int\limits_{0}^{1}{dx} \\\ & \Rightarrow W=\alpha \\\ \end{aligned}$
In this way, we need to find for all the parts,
For the path B to c, the x- coordinate is constant, therefore, the work done is,
$\begin{aligned} & W=\int{2\alpha xdy}=2\alpha \int\limits_{1}^{0.5}{dy} \\\ & \Rightarrow W=-\alpha \\\ \end{aligned}$
For the path c to d, the y coordinate is constant,
Therefore, the work done,
$\begin{aligned} & W=\int{\alpha ydx}=0.5\alpha \int\limits_{1}^{0.5}{dx} \\\ & \Rightarrow W=\dfrac{-\alpha }{4} \\\ \end{aligned}$
Similarly, for path d to e, the x coordinate is constant,
Therefore, the work done,
$\begin{aligned} & W=\int{2\alpha xdy}=2\alpha \int\limits_{0.5}^{0}{dy} \\\ & W=\dfrac{-\alpha }{2} \\\ \end{aligned}$
For the last two parts, the x and y coordinates are respectively zero, and the derivatives too. Therefore, the work done is equal to zero for both the cases.
Hence the total work done is equal to
$\begin{aligned} & W=\alpha -\alpha -\dfrac{\alpha }{4}-\dfrac{\alpha }{2}=-\dfrac{3\alpha }{4} \\\ & \\\ \end{aligned}$
Given,
$\begin{aligned} & \alpha =-1 \\\ & \Rightarrow W=\dfrac{3}{4}J \\\ & \therefore W=\dfrac{3}{4}J=0.75J \\\ \end{aligned}$

Note:
The work done is zero in a given system, when the force and displacement are perpendicular to each other or when force or displacement is equal to zero. The force acting must be constant and should not change with respect to distance. If so, we need to integrate force acting on the body to find out the work done on the body.