Question

A particle is horizontally projected from the top of a tower with a speed of 20 m/s. Find the angle of its velocity with the horizontal after a time of 2 sec. (Take $g = 10{\text{ m/}}{{\text{s}}^2}$ ).
A) 30°
B) 45°
C) 60°
D) ${\tan ^{ - 1}}\left( {\dfrac{5}{4}} \right)$

Answer 1

The particle is in flight after it is projected horizontally from the tower and so the particle can be referred to as a projectile. The velocity of the projectile has a vertical component and a horizontal component acting separately but simultaneously.

Formula used:
The equation of motion gives the final velocity $v$ of an object moving with an acceleration $a$ at an instant $t$ as, $v = {v_0} + at$, ${v_0}$ is the initial velocity of the object.

Complete step by step answer:
Step 1: Sketching a diagram representing the projectile motion of the particle and list the different parameters.

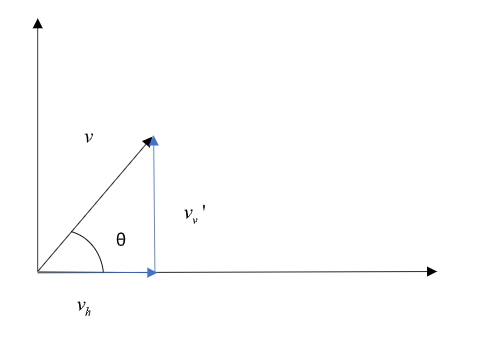
Here, the particle is projected at a speed of $v = 20{\text{m/s}}$ horizontally.
Let ${v_h}$ be the initial horizontal component of the velocity and ${v_v}$ be its initial vertical component.
Then we have, ${v_v} = 0$ and ${v_h} = 20{\text{m/s}}$.
The velocity $v$ makes an angle $\theta$ with the horizontal and it is unknown.
Step 2: Find the angle of the velocity using the equation of motion and trigonometric relations.
During the flight, the vertical component changes due to the force of gravity.
The changed vertical component of the velocity can be obtained by the equation of motion.
The equation of motion gives the final velocity $v$ of an object moving with an acceleration $a$ at an instant $t$ as $v = {v_0} + at$ --------- (1), ${v_0}$ is the initial velocity of the object.
Let ${v_v}'$ be the final velocity in the vertical direction. Also here, acceleration of the particle is the acceleration due to gravity i.e., $a = g$.
The equation (1) can be represented as ${v_v}' = {v_v} + gt$
Substituting the values for ${v_v} = 0{\text{m/s}}$ and $g = 10{\text{m/}}{{\text{s}}^2}$ in equation (1), we obtain the vertical component of the final velocity at $t = 2{\text{s}}$.
i.e., ${v_v}' = 0 + \left( {10 \times 2} \right) = 20{\text{m/s}}$
Thus we have, ${v_v}' = 20{\text{m/s}}$.
We know, $\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$
Now from the figure, we have $\sin \theta = \dfrac{{{v_v}'}}{v}$ and $\cos \theta = \dfrac{{{v_h}}}{v}$. Then $\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{{{v_v}'}}{{{v_h}}}$ ----- (2)
Substituting the values of ${v_v}' = 20{\text{m/s}}$ and ${v_h} = 20{\text{m/s}}$ in equation (2) we get, $\tan \theta = \dfrac{{20}}{{20}} = 1$
Then, $\theta = {\tan ^{ - 1}}1 = 45^\circ$

Therefore, the angle of velocity with the horizontal is $45^\circ$. Hence, option (B) is correct.

Note:
The vertical component of the initial velocity is zero because the particle is said to be projected horizontally. During the flight, the horizontal component remains the same as there is no acceleration acting on the particle along the horizontal but the vertical component of velocity changes as the particle has acceleration due to gravity.