Question

A particle is given an initial speed $u$ inside a smooth spherical shell of radius $R = 1m$ such that it is just able to complete the circle. Acceleration of the particle when its velocity is vertical is:

A) $g\sqrt {10}$
B) $g$
C) $g\sqrt 2$
D) $g\sqrt 6$

Answer 1

To solve this question, we have to calculate the resultant of the tangential and centripetal acceleration. We all know the value of tangential acceleration which is equal to the value of acceleration due to gravity. The centripetal acceleration can be calculated by using velocity and the radius of the circle.

Formulae used:
${v_l} = \sqrt {5gl}$
Here ${v_l}$ is the velocity at the lowest point, $g$ is the acceleration due to gravity and $l$ is distance from center.
$a = \dfrac{{{v^2}}}{r}$
Here $a$ is the centripetal acceleration, $v$ is the tangential velocity at point B and $r$ is the radius of the circle.

Complete step by step solution:
We know that in a circle the velocity at the lowest most position will be,
${v_l} = \sqrt {5gl}$
Here ${v_l}$ is the velocity at the lowest point, $g$ is the acceleration due to gravity and $l$ is the distance.
So, $u = \sqrt {5gl}$

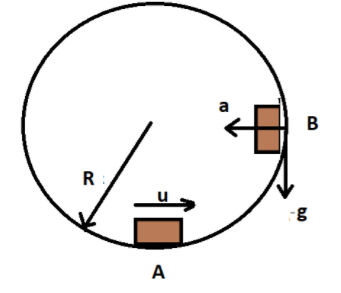
Applying conservation of energy at points A and B, we get
$\Rightarrow \dfrac{1}{2}m{u^2} = \dfrac{1}{2}m{v^2} + m\left( - \right)gl$
Here $u$ is the velocity at point A, $v$ is the velocity at point B, $m$ is the mass of the box, $g$ is the acceleration due to gravity and $l$ is the distance from the center.
The negative sign in gravity is because of its downwards action.
Simplifying the equation, we get,
$\Rightarrow {u^2} = {v^2} - 2gl$
Putting the value of $u$, we get
$\Rightarrow {v^2} = {\left( {\sqrt {5gl} } \right)^2} - 2gl$
$\Rightarrow {v^2} = 3gl$
$\Rightarrow v = \sqrt {3gl}$
So the value of tangential velocity at point B is $\sqrt {3gl}$.
We know that,
$\Rightarrow a = \dfrac{{{v^2}}}{r}$
Here $a$ is the centripetal acceleration, $v$ is the tangential velocity at point B and $r$ is the radius of the circle.
Putting the values of $v$ and $r$, we get
$\Rightarrow a = 3g$

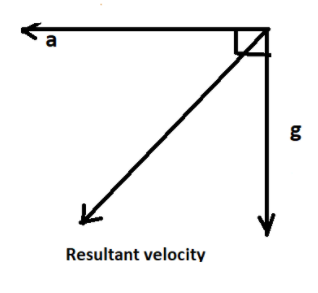
From the above diagram, the resultant acceleration acting on the body will be,
$\Rightarrow {a_{net}} = \sqrt {{a^2} + {g^2} + 2ag\cos 90^\circ }$
$\Rightarrow {a_{net}} = \sqrt {{a^2} + {g^2}}$
Putting the value of $a = 3g$ we get,
$\Rightarrow {a_{net}} = \sqrt {9{g^2} + {g^2}} = g\sqrt {10}$
So the net acceleration acting on the body will be $g\sqrt {10}$.

Hence option (A) is the correct option.

Note: In a vertical circle,
1. The velocity at the lower most position is $v = \sqrt {5gl}$
2. The velocity at the horizontal position is $v = \sqrt {3gl}$
3. The velocity at the top most position is $v = \sqrt {gl}$
Here $g$ is the acceleration due to gravity and $l$ is the distance from the centre. Also for particles in a vertical circle, both centripetal acceleration and acceleration due to gravity acts on it.