Solveeit Logo
Login

Question

Question: A particle is free to move along the x-axis has potential energy given by \(U(x)=k[1-exp^{-x^{2}}]\)...

A particle is free to move along the x-axis has potential energy given by U(x)=k[1−exp−x2]U(x)=k[1-exp^{-x^{2}}] for −∞≤x≤+∞-\infty \leq x\leq +\infty where kk is a positive constant of appropriate dimensions. Then :
A. at points away from the origin, the particle is in unstable equilibrium
B. For any finite non-zero value of xx there is a force directed away from the origin
C. if its total mechanical energy is k2\dfrac{k}{2} it has its minimum kinetic energy at the origin
D. for small displacements from x=0x=0 the motion is simple harmonic

Explanation

Solution

We know that potential energy is the energy posed by the position of the object with respect to the origin. is the Since the given potential energy is in terms of exponents, let us first try to understand the nature of motion of the particle, using a graph which will be discussed below.

Complete step-by-step solution:
Let us consider the given equation U(x)=k[1−exp−x2]U(x)=k[1-exp^{-x^{2}}] for −∞≤x≤+∞-\infty \leq x\leq +\infty where kk is a positive constant .
Now look at
U(0)=k[1−exp−02]U(0)=k[1-exp^{-0^{2}}]
  ⟹  U(0)=0\implies U(0)=0
To under the equation better, let us draw a graph as shown below

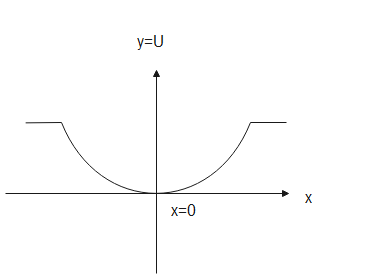
Clearly, from the diagram the particle is stable, for any small displacement the particle will return to its mean position, which is the origin where potential energy is minimum.
Hence clearly A and B is not the answer.
Now look at the force which acts in the particle it is given as
F=−δUδxF=\dfrac{-\delta U}{\delta x}
  ⟹  F=−δk[1−exp−x2]δx\implies F=\dfrac{-\delta k[1-exp^{-x^{2}}]}{\delta x}
  ⟹  F=k[−exp−x2]×−2x\implies F= k[-exp^{-x^{2}}]\times -2x
  ⟹  F=2xk[exp−x2]\implies F=2xk[exp^{-x^{2}}]
From the above we can say that
∴F∝x\therefore F\propto x
Since in SHM also, we have F∝xF\propto x, we can say that the particle undergoes SHM for displacement in the regions near x=0x=0
Thus the correct answer is option D. for small displacements from x=0x=0 the motion is simple harmonic.

Note: We know that SHM or simple harmonic motion is the to and from oscillatory motion of a particle along its mean position, which is x=0x=0 or the origin here. Also note that the total energy of the particle is the sum of its kinetic and potential energy, thus if potential energy is 00 at x=0x=0, then from C, we can say that K.E(0)=K2K.E(0)=\dfrac{K}{2}, however, that is not the minimum kinetic energy possible.