Question
Question: A particle is executing SHM with time period \(T\). Starting from mean position, time taken by it to...
A particle is executing SHM with time period T. Starting from mean position, time taken by it to complete 85 oscillations, is
A. 12T
B. 6T
C. 125T
D. 127T
Solution
To solve the given question we will use the concept of phasor diagram. A phasor diagram is used to represent two or more stationary sinusoidal quantities at any instant of time. The projection of phasor onto an axis at a specific time gives the value of the quantity at that time.
Formula used:
Y=Asinωt
Complete step-by-step answer:
According to phasor diagram concept, we know that
So, Total distance covered by a particle in one oscillation =4A
we will divide this whole path in 8 intervals,
Then, each interval would be of measurement 2A
So, 85 oscillations mean, it has already completed 21 oscillations
i.e. total distance =2A and is halfway to the other side which is 2A.
Equation of SHM is given by, Y=Asinωt; where A= amplitude and ω=T2π
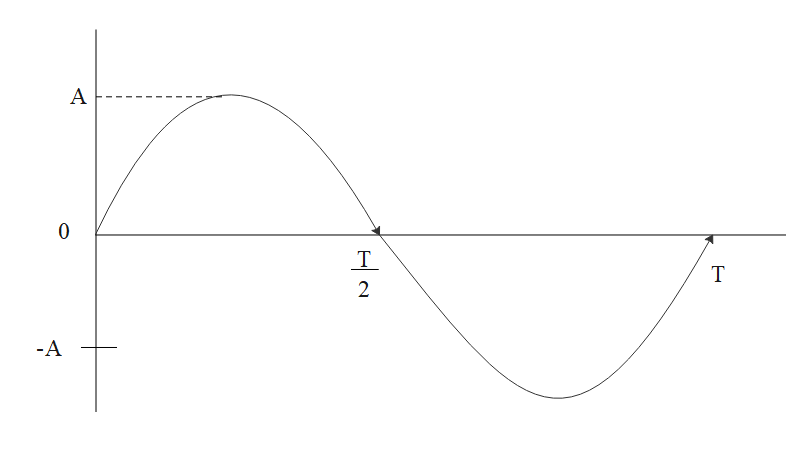
⇒2A=AsinT2π×t
t=12T
Now, substituting t=12T
Total time taken = time to complete previous 21 oscillations + time taken to complete 2A
=2t+12t=127T
So, the correct answer is “Option D”.
Additional Information: Phasor diagrams are used in simple harmonic motion and RLC circuits which have elements that are out of phase with one another and thus difficult to work with in configuration space.
When the motion of a particle performing uniform circular motion is projected onto its diameter, the projection undergoes simple harmonic motion. The circular motion is the representation of SHM in the phase diagram or phasor, and the angular velocity of this circular motion is the frequency of the SHM.
Note: The equation of SHM explicitly represents a sinusoidal function, i.e. it represents a function which varies periodically with time. Amplitude is defined as the maximum displacement. The shortest time taken to complete one oscillation is defined as the time period.
