Question

A particle is executing a Simple Harmonic Motion with a time period $T$. Starting from the mean position, the time taken for it to complete $\dfrac{5}{8}$ oscillations is

Answer 1

The best way to solve this question is by drawing phasor diagrams. A phasor diagram is a diagrammatic representation of the phase difference between sinusoidal with the same frequency. Using phasor diagrams, we can find the relationship between multiple sinusoidal signals of the same frequency.

Complete step by step solution:
Let $A$ be the amplitude of the sinusoidal wave.
The below diagram shows a phasor diagram:

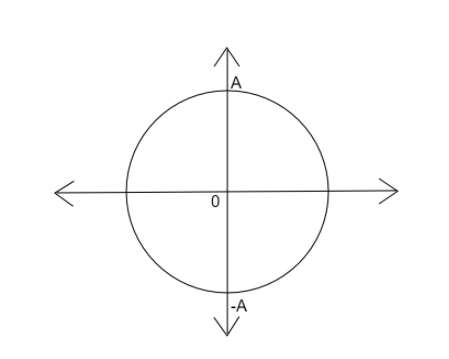
From the above diagram, we know that the total distance covered in one rotation will be $4A$ . Now let us split the path into $8$ intervals. So, each interval will constitute a measurement $\dfrac{A}{2}$ .
We have to find the time taken for it to complete $\dfrac{5}{8}$ oscillations. So now, we can say that the particle has already traveled a distance of half an oscillation plus an additional distance $\dfrac{A}{2}$ . That is, the particle has traveled a distance of $2A$ and an additional distance $\dfrac{A}{2}$ .
Equation of motion of the particle in simple harmonic motion is given by
$Y=A\sin \omega t$
where $\omega$ is the angular frequency given by
$\omega =\dfrac{2\pi }{T}$
Substituting the value of $Y$ as $\dfrac{A}{2}$ and substituting the equation for $\omega$ , we get
$\dfrac{A}{2}=A\sin \dfrac{2\pi }{T}t$
Take sine inverse on both sides and convert degrees to radians. That will give us
$30\times \dfrac{\pi }{180}=\dfrac{2\pi }{T}t$
Evaluating the above equation gives us
$t=\dfrac{T}{12}$
For half an oscillation, the time taken will be $\dfrac{T}{2}$ . Adding both the time taken will give us the total time taken for ${}^{5}/{}_{8}$ oscillations.
$\therefore {{T}_{tot}}=\dfrac{T}{2}+\dfrac{T}{12}$
$\Rightarrow {{T}_{tot}}=\dfrac{7T}{12}$

Therefore, the total time taken to complete $\dfrac{5}{8}$ oscillations is $\dfrac{7T}{12}$.

Note:
To convert degrees to radians, multiply by the degree value by $\dfrac{\pi }{180}$ .
A simple harmonic motion is a motion where a particle goes back and forth from a mean position such that the acceleration is proportional to the distance from this mean position. A simple harmonic mot function always represents a sinusoidal function with constant frequency and maximum amplitude.