Question

A particle falls freely near the surface of the Earth. Consider a fixed point O (not vertically below the particle) on the ground:
A) Angular momentum of the particle O is increasing.
B) Torque of the gravitational force on particle O is decreasing.
C) The moment of inertia of the particle about O is decreasing.
D) The angular velocity of the particle about O is increasing.

Answer 1

Recall the concept of linear momentum. The linear momentum of a particle is associated with motion in a line or a plane. But angular momentum is a vector quantity, that is related to the rotational motion of a rotating body.

Step-By-Step Explanation:
Step I:
Angular momentum can be calculated by taking the product of the angular velocity and its moment of inertia. Moment of inertia is the product of mass and the radius of the object. Angular momentum is written as $L = mvr$ ---(i)
$L$ is the angular momentum
$m$ is the mass
$v$ is the velocity
$r$ is the radius or the distance

Step II:
Given the fixed point is O, let ‘d’ be the distance of the object. The magnitude of angular momentum about the point O is given by$= mvd$ ---(ii)
When the particle is falling on the ground, its velocity will increase. Therefore angular momentum will also increase.

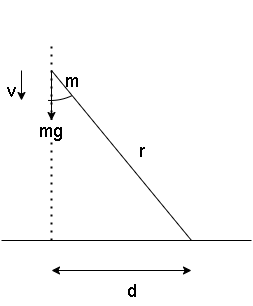
Step III:
The velocity is increasing due to the gravitational pull or the gravitational force. Therefore, $v = g$
Equation (ii) becomes
Magnitude of angular momentum about O$= mgd$

Step IV:
Given that the body is falling freely, therefore external force or torque will be applied to change its angular momentum. The amount of torque required depends on the moment of inertia of the body. The moment of inertia is given by $m{r^2}$
Where $m$ is the mass of the particle and $r$ is the distance.

Step V: When the body will fall freely about point O, its distance from the axis of rotation will decrease. When the distance decreases, then the moment of inertia also decreases. So the moment of inertia of the freely falling body about point O will decrease.

Step VI:
Angular velocity is given by $\omega = \dfrac{{v\sin \theta }}{r}$
It is clear that the radius or the distance of the particle will decrease and velocity will increase. Therefore angular velocity of the particle about O increases.

Option D is the right answer.

Note: It is to be noted that the terms rotational motion and circular motion are not the same. Circular motion is caused when the object or the body is moving around some other body. But rotational motion is produced when the body moves about its own axis.