Question

A particle executes simple harmonic motion with a frequency of 2.5 Hz and an amplitude of 2 m. Find the speed of the particle at 0.3 sec after it crosses the equilibrium position.
A) Zero.
B) $2\pi {\text{m}}{{\text{s}}^{ - 1}}$
C) $4\pi {\text{m}}{{\text{s}}^{ - 1}}$
D) $\pi {\text{m}}{{\text{s}}^{ - 1}}$

Answer 1

A particle executing simple harmonic motion will have a maximum speed at the equilibrium position whereas its speed will be zero at the extreme positions. The period of the motion of the particle will be the reciprocal of its frequency.

Formula used:
-The period of oscillation of a simple harmonic motion is given by, $T = \dfrac{1}{f}$ where $f$ is the frequency of the oscillation.

Complete step by step answer.
Step 1: Sketch a rough figure describing the simple harmonic motion of the particle and list the parameters mentioned in the question.

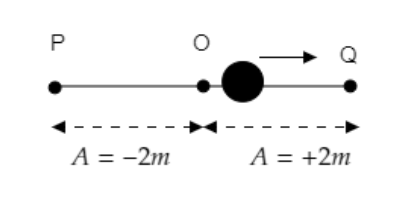
The above figure represents the simple harmonic motion of the particle.
Its two extreme positions are marked as P and Q. The point O represents the equilibrium position.
The amplitude of the motion is $A = 2{\text{m}}$ and the frequency of the oscillation is $f = 2.5{\text{Hz}}$.
Step 2: Express the relation for the period of the motion and find the period by substitution.
The period of oscillation of a simple harmonic motion is given by, $T = \dfrac{1}{f}$ --------- (1) where $f$ is the frequency of the motion.
Substituting for $f = 2.5{\text{Hz}}$ in equation (1) we get, $T = \dfrac{1}{{2.5}} = 0.4{\text{sec}}$
Thus the period of the motion is $T = 0.4{\text{sec}}$ .
The given time $t = 0.3{\text{sec}}$ at which the speed is to be determined can also be expressed as $t = \dfrac{{3T}}{4}$
Step 3: From the figure, predict the position of the particle when $t = \dfrac{{3T}}{4}$ .
Suppose the particle is initially at rest at the time $t = 0{\text{sec}}$ and starts to swing to its right as shown in the figure.

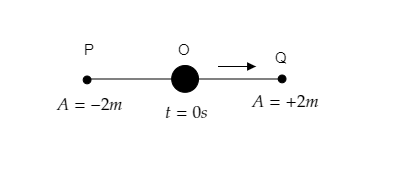
So at the time $t = \dfrac{T}{4}$, it will be at point Q as shown in the figure below.

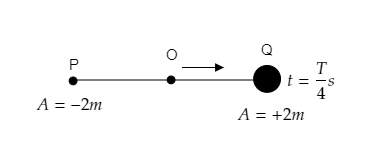
Then at the time, $t = \dfrac{{2T}}{4}$ it will be at O as shown in the figure below.

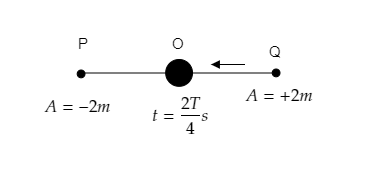
At the time $t = \dfrac{{3T}}{4}$ it will be at P as shown in the figure below.

So, at the given time $t = 0.3{\text{sec}} = \dfrac{{3T}}{4}$, the particle is at its extreme left.
If the particle were to initially swing to the left, the particle would be at its extreme right at the given time $t = 0.3{\text{sec}}$. The speed of the particle is zero at both extremes.
Thus the speed of the particle will be zero.

So the correct option is A.

Note: Alternate method
The displacement of the particle executing simple harmonic motion can be represented as $x = A\sin \left( {2\pi ft} \right)$ ------- (A)
Substituting for $A = 2{\text{m}}$ and $f = 2.5{\text{Hz}}$ in equation (A) we get, $x = 2\sin \left( {5\pi t} \right)$
At $t = 0.3{\text{sec}}$, the displacement of the particle will be $x = 2\sin \left( {1.5\pi } \right)$
The argument of the sine term can be expanded to get, $x = 2\sin \left( {\pi + \dfrac{\pi }{2}} \right)$
Since $\sin \left( {\pi + \theta } \right) = - \sin \theta$, the above expression becomes $x = - 2\sin \dfrac{\pi }{2} = - 2{\text{m}}$
Therefore at $t = 0.3{\text{sec}}$ the displacement of the particle is $x = - 2{\text{m}} = - {\text{A}}$
The displacement suggests that the position of the particle is at the extreme left. Since the speed at any extrema is zero for S.H.M, the speed at $t = 0.3{\text{sec}}$ will be zero.