Question

A particle executes simple harmonic motion between $x=-A$ and $x=+A$. The time taken by it to go from 0 to $\dfrac{A}{2}$ is ${{T}_{1}}$ and to go from $\dfrac{A}{2}$ to A is ${{T}_{2}}$. Then
A.)${{T}_{1}} < {{T}_{2}}$
B.)${{T}_{1}} > {{T}_{2}}$
C.)${{T}_{1}} = {{T}_{2}}$
D.)${{T}_{1}} = 2{{T}_{2}}$

Answer 1

Hint: We can calculate the time period of each stage by using the simple harmonic wave equation. We can assign the given displacement to the equation. Thereby, we will get the condition of time period at each stage. By calculating two time periods we can find the ratio between them.

Formula used:
$x=A\sin \omega t$, where A is the maximum displacement, $\omega$ is the angular frequency and t is the time period.

Complete step by step answer:

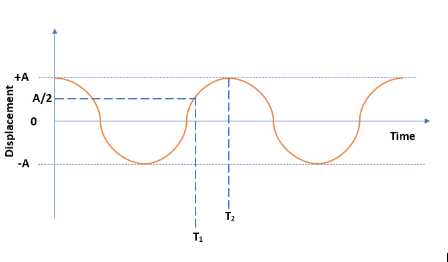
The above diagram shows the displacement-time graph of simple harmonic motion. The particle executes simple harmonic motion between $x=-A$ and $x=+A$. As we know, the displacement of simple harmonic motion can be written as,

$x=A\sin \omega t$…………………..(1), A is the maximum displacement, $\omega$ is the angular frequency and t is the time period.

As per the question after time ${{T}_{1}}$, the displacement of the particle will be $\dfrac{A}{2}$. We can substitute this into the equation (1).

$\dfrac{A}{2}=A\sin \omega {{T}_{1}}$

Therefore,

$\dfrac{1}{2}=\sin \omega {{T}_{1}}$

From this, we can say that,

$\omega {{T}_{1}}=\dfrac{\pi }{6}$
${{T}_{1}}=\dfrac{\pi }{6\omega }$……………………….(2)

Next, we can find the time period ${{T}_{2}}$. ${{T}_{2}}$ is the time period to move from $\dfrac{A}{2}$ to A. If t is representing the time period required to move a particle from 0 to A. Then we can write ${{T}_{2}}$ as,

${{T}_{2}}=t-{{T}_{1}}$

We can plug these values to the equation (1).

$A=A\sin \omega t$

Therefore,

$\sin \omega t=1$
$\omega t=\dfrac{\pi }{2}$
$t=\dfrac{\pi }{2\omega }$
Since ${{T}_{2}}=t-{{T}_{1}}$, the ${{T}_{2}}$ will be,
${{T}_{2}}=\dfrac{\pi }{2\omega }-\dfrac{\pi }{6\omega }$
${{T}_{2}}=\dfrac{4\omega \pi }{12{{\omega }^{2}}}$
${{T}_{2}}=\dfrac{\pi }{3\omega }$……………………(3)

Now, we can compare the equation (2) and equation (3), to find which time is larger.

So,

$\dfrac{{{T}_{1}}}{{{T}_{2}}}=\dfrac{\dfrac{\pi }{6\omega }}{\dfrac{\pi }{3\omega }}$
$\dfrac{{{T}_{1}}}{{{T}_{2}}}=\dfrac{1}{2}$

Here, we can see the time period ${{T}_{2}}$ is greater than the ${{T}_{1}}$. For a simple harmonic motion, the velocity of the particle will be maximum at its mean position and it decreases when the particle moves towards the extreme point. That’s why the first half of the displacement requires less time to travel than the second half.

So, the correct answer is option A.

Note: If we are using ${{T}_{2}}$ directly in the simple harmonic wave equation, then the displacement has to be $\dfrac{A}{2}$. Since ${{T}_{2}}$ is the time period when the particle moves from $\dfrac{A}{2}$ to A. That’s why we are using total time period t. Then we are subtracting ${{T}_{1}}$ from t to get the ${{T}_{2}}$ time period. It is better to draw the displacement-time graph of simple harmonic motion. From the graph itself, we can understand the answer to the question.