Question

A particle executes SHM with time period T and amplitude A. The maximum possible average velocity in time $\dfrac{T}{4}$​ is
$A.\dfrac{{2A}}{T} \\\ B.\dfrac{{4A}}{T} \\\ C.\dfrac{{8A}}{T} \\\ D.\dfrac{{4\sqrt 2 A}}{T} \\\$

Answer 1

In order to solve this problem we need to know that in the time T the particle starts again from the initial points towards the same direction. The particle executes the max velocity at the mean position and the minimum velocity is at extreme position. We also need to know that the average velocity is the distance travelled upon time taken. Assume this SHM as circular, so that one can get the velocity. Doing this will solve your problem.

Complete answer:
We will draw the circle and then we will assume it as SHM and then we will consider the time period and amplitude.
The figure for this problem can be drawn as:

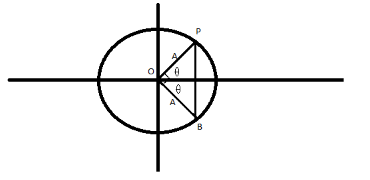
The radius of the circle is amplitude and it is A.
We have assumed the SHM as circular. Since in one T it completes one circle so in one fourth of T it will complete on a quarter circle so we have considered the quarter circle here.

When the particle completes one circle ($2\pi$) then the time it takes is T.
So, in the time $\dfrac{T}{4}$ it covers the angle $\dfrac{{2\pi }}{4} = \dfrac{\pi }{2}$.
We know that PB = 2Asin$\theta$.
As the angle POB is 90 and it is bisected so, here $\theta = \dfrac{\pi }{4}$.
So, PB = 2Asin$\dfrac{\pi }{4}$=2A$\left( {\dfrac{1}{{\sqrt 2 }}} \right) = \dfrac{{2A}}{{\sqrt 2 }} = \sqrt 2 A$.
So, the average velocity is total distance PB upon the time taken that is one fourth of T.
So, we get the average velocity as $\dfrac{{\sqrt 2 A}}{{\dfrac{T}{4}}} = \dfrac{{4\sqrt 2 A}}{T}$.

So, the correct answer is “Option D”.

Note:
When you get to solve the problems in SHM you need to know that In mechanics and physics, simple harmonic motion is a special type of periodic motion where the restoring force on the moving object is directly proportional to the object's displacement magnitude and acts towards the object's equilibrium position. Doing this will solve your problem and will give out the right answer.