Question

A particle describes a horizontal circle on the smooth surface of an inverted cone. The height of the plane of the circle above the vertex is $9.8cm$. Find the speed of the particle.
A. $0.98m/s$
B.L $1.96m/s$
C. $0.49m/s$
D. $3.92m/s$

Answer 1

Here, it is given that the particle is moving in a horizontal circular path on the smooth surface of an inverted cone. Therefore, we need to use the concept of uniform circular motion and its equations to get the relation between the height of the plane of the circle above the vertex and speed and then find the answer by using the given value.

Formula used:
${F_c} = \dfrac{{m{v^2}}}{r}$, where ${F_c}$is the centrifugal force, $m$is mass of the particle, $v$ is speed of the particle and $r$ is the radius of the path of the particle
$W = mg$, where $W$is weight of the particle, $m$is mass of the particle and $g$is the gravitational acceleration
${N_x} = N\sin \theta$, where ${N_x}$is horizontal component of normal force, $N$is the normal force acting on the particle and $\theta$ is the angle made by conical surface with horizontal
${N_y} = N\cos \theta$, where ${N_y}$ is vertical component of normal force, $N$is the normal force acting on the particle and $\theta$ is the angle made by conical surface with horizontal

Complete step by step answer:
First, let us see the diagram of given case:

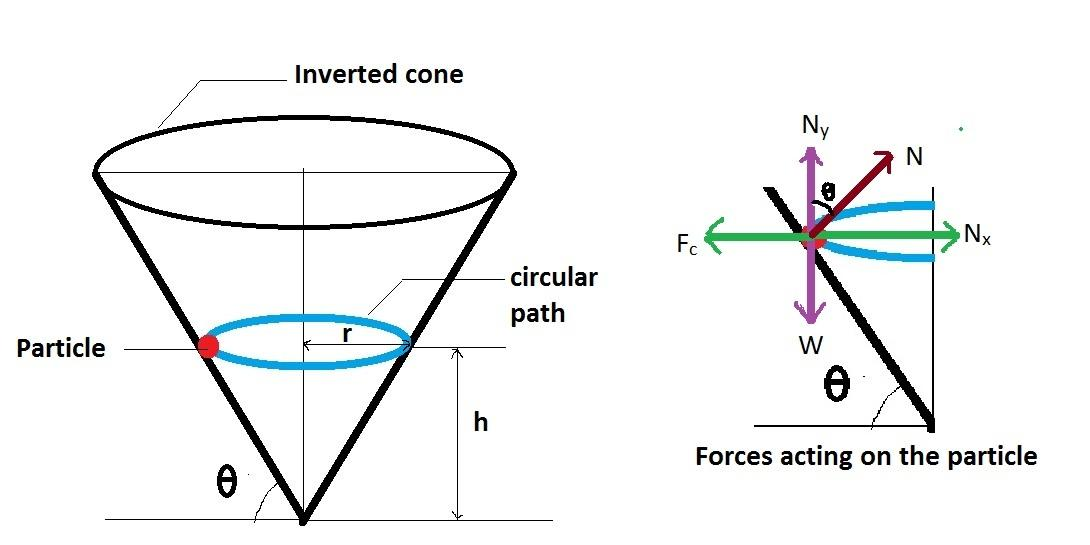
As shown in the diagram, a particle travels on a horizontal circle on the smooth surface of an inverted cone.
There are three main forces of action on the particle: Its own weight, centrifugal force and normal force perpendicular to the conical surface.
In equilibrium condition, weight of the particle is balanced by the vertical component of the normal force and centrifugal force is balanced by the horizontal component of the normal force as shown in diagram.
So, we can say that

$${N_x} = {F_c} \Rightarrow N\sin \theta = \dfrac{{m{v^2}}}{r} \\\ {N_y} = W \Rightarrow N\cos \theta = mg \\\$$

Now dividing the horizontal component of the normal force by its vertical component, we get

$$\dfrac{{N\sin \theta }}{{N\cos \theta }} = \dfrac{{\dfrac{{m{v^2}}}{r}}}{{mg}} \\\ \Rightarrow \tan \theta = \dfrac{{{v^2}}}{{rg}} \\\$$

But, from the diagram, it is clear that
$\tan \theta \Rightarrow \dfrac{h}{r}$

$$\Rightarrow \dfrac{{{v^2}}}{{rg}} = \dfrac{h}{r} \\\ \therefore v = \sqrt {gh} \\\$$ $$\Rightarrow \dfrac{{{v^2}}}{{rg}} = \dfrac{h}{r} \\\ \therefore v = \sqrt {gh} \\\$$

It is given that the height of the plane of the circle above the vertex is $9.8cm = 0.098m$
We know that value of gravitational acceleration $g = 10m/{s^2}$

$$\Rightarrow v = \sqrt {10 \times 0.098} \\\ \Rightarrow v = \sqrt {0.98} \\\ \therefore v = 0.98m/s \\\$$

So, the correct answer is “Option A”.

Note:
In this question we have given the height of the plane of the circle above the vertex and we determined the value of speed of the particle. Similarly, if the speed of the particle is given, then the height can be determined by using the same formula $v = \sqrt {gh}$.