Question

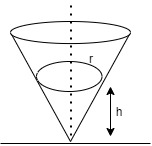
A particle describes a horizontal circle of radius $'r'$ on a smooth surface of an inverted cone. The height of the plane of the circle above the vertex is $'h'$ . Then the speed of the particle will be.

Answer 1

When a particle moves in a circular path it feels forces like centrifugal force and force due to its weight.
Centrifugal force: It is an inertial force that appears to act on all objects when viewed in a rotating frame of reference. It is gives by $\dfrac{m{{v}^{2}}}{r}$

Complete step by step solution
Let us consider a particle moving in a circular path and it is mounted on a smooth surface of an Inverted cone. The height of the plane of the circle from the vertex is $'h'$ .
The particle experiences centrifugal force and force due to its weight.
Centrifugal force is$=\dfrac{m{{v}^{2}}}{r}$
Force due to its weight$=mg$
When particle reaches at the surface of the cone we draw a normal $'N'$ and its component is $N\text{ cos}\theta ,N\sin \theta$
Now, we have two vertical components and two transverse components.
From geometry of figure:

$N\text{ cos}\theta =\dfrac{m{{v}^{2}}}{r}$ ……. (1)
And
$N\sin \theta =mg$ …… (2)
Now,
Divide (1) by (2)
$\dfrac{N\text{ cos}\theta }{N\text{ sin}\theta }=\dfrac{m{{v}^{2}}}{r}/mg=\dfrac{\text{cos}\theta }{\sin \theta }=\dfrac{{{v}^{2}}}{rg}$
$\cot \theta =\dfrac{{{v}^{2}}}{rg}$
In our case,$\cot \theta =\dfrac{h}{r}$
This equation becomes
$\begin{aligned} & \dfrac{h}{r}=\dfrac{{{v}^{2}}}{rg}={{v}^{2}}=hg \\\ & \text{ }v=\sqrt{hg} \\\ & \text{This is speed of the particle}\text{.} \\\ \end{aligned}$

Note: From this discussion, we can find the time revolution of particles by using the value of ‘speed’.
$T=\dfrac{2\pi r}{v}$
Concept of forces should be clear. Knowledge of how they are acting on particles should be clear. Knowledge of trigonometric concepts is needed in such questions.