Question

A particle charge per unit mass $\alpha$ is released from origin $\overline V = {V_0}\widehat i$ in a uniform magnetic field $\overline B = {B_0}\widehat k$ . If the particle passes through $(0,y,0)$ then $y$ is equal to:
(A) $\dfrac{{ - 2{V_0}}}{{{B_0}\alpha }}$
(B) $\dfrac{{{V_0}}}{{{B_0}\alpha }}$
(C) $\dfrac{{2{V_0}}}{{{B_0}\alpha }}$
(D) $\dfrac{{ - {V_0}}}{{{B_0}\alpha }}$

Answer 1

Hint : The particle charge per unit mass is given by $\alpha = \dfrac{q}{m}$ , this particle moving from origin from ${V_0}$ and a force must be acting on that particle while it is moving in the uniform magnetic field. Here, we have to use the concept of Lorentz’s force acting on the particle.

Complete Step By Step Answer:
Let us draw the suitable diagram as per our knowledge of forces acting on the particle in the magnetic field which is directed inside the plane denoted by $z$ in the diagram below.
The particle is starting to move from the point ${V_0}$ along the circular orbit in the $x - y$ plane. The centripetal force lets ${F_m}$ act on the body to move it on the circular orbit.

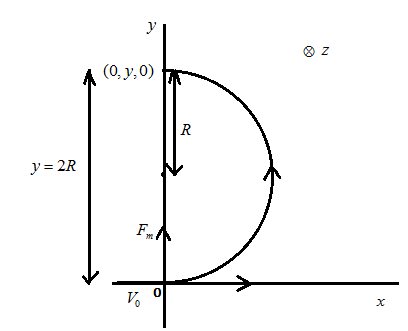
Here we have to use the concept of Lorentz force as
${F_m} = q{V_0}{B_0}$ …. $(1)$
But, as the force ${F_m}$ is the centripetal force acting on the body towards the center in $x - y$ plane is given by:
${F_m} = \dfrac{{m{V_0}^2}}{R}$ ….( $R$ be the radius of the circular orbit of the particle) $(2)$
Now from equating $(1)$ and $(2)$ we get,
$\Rightarrow \dfrac{{m{V_0}^2}}{R} = q{V_0}{B_0}$
$\Rightarrow R = \dfrac{{m{V_0}}}{{q{B_0}}}$
$\Rightarrow R = \dfrac{{{V_0}}}{{\alpha {B_0}}}$ …..(since $\alpha = \dfrac{q}{m}$ ) $(3)$
Now we have to find out the value of $y$ in $(0,y,0)$
For this we have the radius of the circular path along $y$ direction
$\therefore y = 2R$
$\Rightarrow y = \dfrac{{2{V_0}}}{{\alpha {B_0}}}$
Thus, we have calculated the value of $y$ as $\dfrac{{2{V_0}}}{{\alpha {B_0}}}$
The correct answer is the option C.

Note :
Here, we have used the concept of the Lorentz force acting on a charged particle. It is defined as the force exerted on a charged particle $q$ moving with velocity v through an electric field $E$ and magnetic field $B$ . The entire electromagnetic force $F$ on the charged particle.