Solveeit Logo
Login

Question

Question: A particle 'A' starts from 'O' moving along a straight line with constant velocity 'v'. Another part...

A particle 'A' starts from 'O' moving along a straight line with constant velocity 'v'. Another particle 'B', situated 'ℓ\ell' distance away from O, (as shown in figure) also starts moving simultaneously with same speed 'v'. The direction of B is towards A at any instant. Select the correct option:-

A

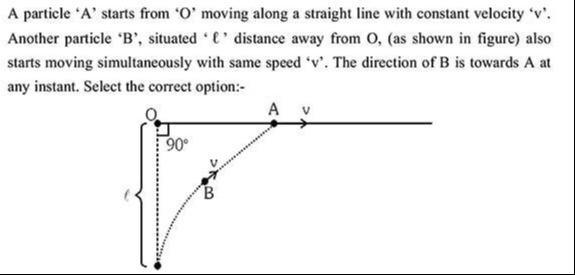
The distance covered by 'B' on y-axis is ℓ/2\ell/2.

B

The time for both the particle to meet each other is ℓ/v\ell/v.

C

The distance covered by 'B' on x-axis is ℓ\ell.

D

The distance covered by 'B' on y-axis is ℓ\ell.

Answer

The distance covered by 'B' on y-axis is ℓ\ell.

Explanation

Solution

Let the origin O be at (0,0). Particle A starts from O and moves along the x-axis with velocity v⃗A=vi^\vec{v}_A = v \hat{i}. Its position at time t is r⃗A(t)=vti^\vec{r}_A(t) = vt \hat{i}.

Particle B starts from a point ℓ\ell distance away from O. From the figure, the initial position of B is (0,−ℓ)(0, -\ell). So, r⃗B(0)=−ℓj^\vec{r}_B(0) = -\ell \hat{j}.

Particle B moves with speed v, and its direction is always towards A. Let the position of B at time t be r⃗B(t)=xB(t)i^+yB(t)j^\vec{r}_B(t) = x_B(t) \hat{i} + y_B(t) \hat{j}.

The velocity of B is v⃗B(t)=vr⃗A(t)−r⃗B(t)∣r⃗A(t)−r⃗B(t)∣\vec{v}_B(t) = v \frac{\vec{r}_A(t) - \vec{r}_B(t)}{|\vec{r}_A(t) - \vec{r}_B(t)|}.

v⃗B=dxBdti^+dyBdtj^=v(vt−xB)i^−yBj^(vt−xB)2+yB2\vec{v}_B = \frac{dx_B}{dt} \hat{i} + \frac{dy_B}{dt} \hat{j} = v \frac{(vt - x_B)\hat{i} - y_B\hat{j}}{\sqrt{(vt - x_B)^2 + y_B^2}}.

This gives the differential equations:

dxBdt=vvt−xB(vt−xB)2+yB2\frac{dx_B}{dt} = v \frac{vt - x_B}{\sqrt{(vt - x_B)^2 + y_B^2}}

dyBdt=−vyB(vt−xB)2+yB2\frac{dy_B}{dt} = -v \frac{y_B}{\sqrt{(vt - x_B)^2 + y_B^2}}

with initial conditions xB(0)=0x_B(0) = 0 and yB(0)=−ℓy_B(0) = -\ell.

Consider the relative motion of B with respect to A. The relative velocity is v⃗B/A=v⃗B−v⃗A\vec{v}_{B/A} = \vec{v}_B - \vec{v}_A.

The direction of v⃗B\vec{v}_B is always towards A. So, in the frame of A, the velocity of B always points towards A.

Let's consider the motion in the reference frame of A. In this frame, A is at rest at the origin. The initial position of B in this frame is r⃗B/A(0)=r⃗B(0)−r⃗A(0)=(0,−ℓ)−(0,0)=(0,−ℓ)\vec{r}_{B/A}(0) = \vec{r}_B(0) - \vec{r}_A(0) = (0, -\ell) - (0,0) = (0, -\ell).

The velocity of B in this frame is v⃗B/A=v⃗B−v⃗A\vec{v}_{B/A} = \vec{v}_B - \vec{v}_A.

The direction of v⃗B\vec{v}_B is towards A.

Let's consider the component of the relative velocity along the line BA.

The rate of change of the distance between A and B, r=∣r⃗A−r⃗B∣r = |\vec{r}_A - \vec{r}_B|, is given by drdt=(r⃗A−r⃗B)∣r⃗A−r⃗B∣⋅(v⃗A−v⃗B)=r^B→A⋅(v⃗A−v⃗B)\frac{dr}{dt} = \frac{(\vec{r}_A - \vec{r}_B)}{|\vec{r}_A - \vec{r}_B|} \cdot (\vec{v}_A - \vec{v}_B) = \hat{r}_{B \to A} \cdot (\vec{v}_A - \vec{v}_B).

Since v⃗B=vr^B→A\vec{v}_B = v \hat{r}_{B \to A}, we have drdt=r^B→A⋅v⃗A−r^B→A⋅(vr^B→A)=r^B→A⋅v⃗A−v\frac{dr}{dt} = \hat{r}_{B \to A} \cdot \vec{v}_A - \hat{r}_{B \to A} \cdot (v \hat{r}_{B \to A}) = \hat{r}_{B \to A} \cdot \vec{v}_A - v.

Let θ\theta be the angle between v⃗A\vec{v}_A and the line BA. Then r^B→A⋅v⃗A=∣v⃗A∣cos⁡θ=vcos⁡θ\hat{r}_{B \to A} \cdot \vec{v}_A = |\vec{v}_A| \cos \theta = v \cos \theta.

So, drdt=vcos⁡θ−v=v(cos⁡θ−1)\frac{dr}{dt} = v \cos \theta - v = v(\cos \theta - 1).

Now consider the component of the velocity of B perpendicular to the line joining O and A (the x-axis).

The initial y-coordinate of B is yB(0)=−ℓy_B(0) = -\ell.

The y-component of the velocity of B is dyBdt=−vyB(vt−xB)2+yB2\frac{dy_B}{dt} = -v \frac{y_B}{\sqrt{(vt - x_B)^2 + y_B^2}}.

Let's consider the component of velocity of B along the y-axis.

The initial velocity of B is towards A, and at t=0, A is at O. So, v⃗B(0)\vec{v}_B(0) is towards O. If B starts at (0,−ℓ)(0, -\ell), then the initial velocity is along the positive y-axis, v⃗B(0)=vj^\vec{v}_B(0) = v \hat{j}.

However, the figure shows the initial position of B at (0,−ℓ)(0, -\ell) and the direction of B towards A at any instant. At t=0, A is at O(0,0). So the direction of B is towards O. This means the initial velocity of B is along the positive y-axis.

Let's consider the projection of the displacement of B on the initial line OB (the y-axis).

Let yy be the y-coordinate of B at time t. Initially y(0)=−ℓy(0) = -\ell. The initial velocity of B is along the positive y-axis, with magnitude v.

The component of velocity of B along the y-axis is dydt\frac{dy}{dt}.

The direction of v⃗B\vec{v}_B is from B to A.

Let ϕ\phi be the angle between the line BA and the positive x-axis. The vector BA is (vt−xB,−yB)(vt - x_B, -y_B).

The angle between v⃗B\vec{v}_B and the positive y-axis is ϕ−π/2\phi - \pi/2.

dyBdt=vsin⁡(ϕ−π/2)=−vcos⁡ϕ\frac{dy_B}{dt} = v \sin(\phi - \pi/2) = -v \cos \phi.

cos⁡ϕ=vt−xB(vt−xB)2+yB2\cos \phi = \frac{vt - x_B}{\sqrt{(vt - x_B)^2 + y_B^2}}.

dyBdt=−vvt−xB(vt−xB)2+yB2\frac{dy_B}{dt} = -v \frac{vt - x_B}{\sqrt{(vt - x_B)^2 + y_B^2}}.

Let's consider the component of the velocity of B parallel to the initial line OB (y-axis).

The initial line OB is along the negative y-axis.

The component of v⃗B\vec{v}_B along the negative y-axis is −dyBdt=−v−yB(vt−xB)2+yB2=vyB(vt−xB)2+yB2-\frac{dy_B}{dt} = -v \frac{-y_B}{\sqrt{(vt - x_B)^2 + y_B^2}} = v \frac{y_B}{\sqrt{(vt - x_B)^2 + y_B^2}}.

The initial value of this component is v−ℓ02+(−ℓ)2=v−ℓℓ=−vv \frac{-\ell}{\sqrt{0^2 + (-\ell)^2}} = v \frac{-\ell}{\ell} = -v.

This is the component along the positive y-axis is v.

The total distance traveled by B along the y-axis is ℓ\ell.