Solveeit Logo
Login

Question

Question: A part of circuit in steady state along with the currents flowing in the branches, the value of resi...

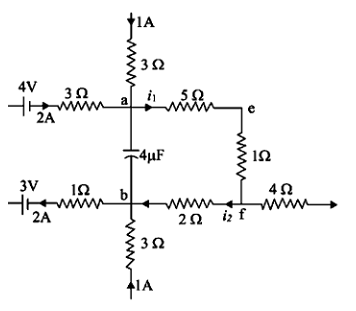
A part of circuit in steady state along with the currents flowing in the branches, the value of resistances etc., is shown in figure. Calculate the energy stored in the capacitor.

A.8×10−1JA. 8\times 10^{-1}J
B.8×10−2JB.8\times {{10}^{-2}}J
C.8×10−3JC.8\times {{10}^{-3}}J
D.8×10−4JD.8\times {{10}^{-4}}J

Explanation

Solution

Hint: In order to know the energy of a capacitor, we need to know the voltage across a capacitor. To find the voltage across the capacitor in the given circuit we will use Kirchhoff’s voltage and current laws at different parts of the circuit. Therefore, the energy stored in the capacitor can be found easily.

Formula used:
E=12CV2E=\dfrac{1}{2} CV^2

Complete step by step solution:
Kirchhoff’s current law states that the total algebraic sum of currents in any point in the circuit is basically zero. Actually, we have to put positive signs for currents coming inside the point and negative signs for currents going outwards from the point. Or we may assume the opposite as well, but the answer will be the same. Applying this law at the point a, in the given circuit, we
obtain,
1A+2A−i1=01A+2A-i_1=0
This gives, i1=3Ai_1=3A.
Similarly, applying this law at the point b we get,
i2+1A=2Ai_2+1A=2A
This gives, i2=1Ai_2=1A .
Now, Kirchhoff’s voltage law is applicable for a loop in the circuit. It states that the algebraic
the sum of the voltage in any loop of a circuit is zero. Now applying this law in the loop (‘aefb’) of
the given circuit, we get,
V=5i1+1i1+2i2=20V=5{{i}_{1}}+1{{i}_{1}}+2{{i}_{2}}=20Volt
Here, V is the voltage across the capacitor, which is found to be 20 volts by our calculation.
Now the energy stored in the capacitor is given by,
E=12CV2=12.4×10−6.(20)2=8×10−4JE=\dfrac{1}{2}CV^2=\dfrac{1}{2}.4\times 10^{-6} .(20)^2=8\times 10^{-4} J
After doing the calculation we find out that option D is the correct answer.
Additional information:
Kirchhoff’s current law is another form of the law of conservation of electric charge. On the other hand, Kirchhoff’s voltage law is another form of the law of conservation of energy.

Note: While putting different values in Kirchhoff’s law, keep in mind the signs of different terms. When the resistance is given in ohm and the current is given in Ampere, the voltage will be obtained in Volt. If current were given in milli-ampere, the voltage would be in milli-volt, and 1milli =10−3={{10}^{-3}}. So, the answer will change in terms of power of 10.