Question
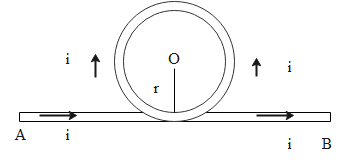
Question: A part of a long wire A carrying a current I is bent into a circle of radius r as shown in the figur...
A part of a long wire A carrying a current I is bent into a circle of radius r as shown in the figure. The net magnetic field at the centre O of the circular loop is
Solution
The net magnetic field at the centre O of the circular loop is the sum of the magnetic field due to the circular part of the wire and the magnetic field due to the straight part of the wire. So, we will add the magnetic fields of the circular part and the straight part of the wires.
Formula used:
B=2πrμ0i
B=2rμ0i
Complete step by step solution:
At the centre O of the circular loop, the magnetic field due to the straight part of the wire is given as follows.
B1=2πrμ0i
In this case, ‘r’ represents the distance between the centre O and the straight wire.
At the centre O of the circular loop, the magnetic field due to the circular part of the wire is given as follows.
B2=2rμ0i
In this case, ‘r’ represents the radius of the circular loop.
Therefore, the net magnetic field at the centre O of the circular loop is the sum of the magnetic field due to the circular part of the wire and the magnetic field due to the straight part of the wire.
Thus, the net magnetic field at the centre O of the circular loop is,
B=B1+B2
Now substitute the expressions of the magnetic fields in the above equation.
