Solveeit Logo
Login

Question

Question: A parallelogram circumscribes the ellipse and two of its opposite angular points lie on the straight...

A parallelogram circumscribes the ellipse and two of its opposite angular points lie on the straight lines x2=h2{{x}^{2}}={{h}^{2}} ; prove that the locus of the other two is the conic
x2a2+y2b2(1−a2h2)=1\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}\left( 1-\dfrac{{{a}^{2}}}{{{h}^{2}}} \right)=1.

Explanation

Solution

Hint: Find vertices of parallelogram by intersection of tangents (sides of parallelogram) using parametric coordinates of point of contacts.

We have ellipse given;
x2a2+y2b2=1................(i)\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1................\left( i \right)
As, given in question, two of the angular points of parallelogram is lying on x2=h2{{x}^{2}}={{h}^{2}}.


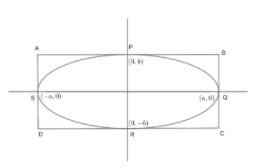
ABCDABCDis a parallelogram.
Let AB,BC,CD,DAAB,BC,CD,DA is touching ellipse at points P,Q,R,SP,Q,R,S respectively. In other language, we can say that two tangents are drawn from points P and S,P\text{ and }S, two tangents are from P and Q,P\text{ and }Q, two from Q and R;Q\text{ and }R; similarly, two tangents from R and S,R\text{ and }S, which are intersecting at A,B,C&DA,B,C\And D respectively.
Let two points which are lying on x2=h2{{x}^{2}}={{h}^{2}}are BBand DD.
Let point P and QP\text{ and }Q is (acos⁡α,bsin⁡α)\left( a\cos \alpha ,b\sin \alpha \right) and (acos⁡β,bsin⁡β)\left( a\cos \beta ,b\sin \beta \right) as parametric coordinates on ellipse x2a2+y2b2=1.\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1.
We know that tangent from any point (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) on ellipse is;
T=0T=0
Or xx1a2+yy1b2=1\dfrac{x{{x}_{1}}}{{{a}_{2}}}+\dfrac{y{{y}_{1}}}{{{b}_{2}}}=1
Hence, tangents through P(acos⁡α,bsin⁡α)P\left( a\cos \alpha ,b\sin \alpha \right) and Q(acos⁡β,bsin⁡β)Q\left( a\cos \beta ,b\sin \beta \right);
xcos⁡αa+ysin⁡αb=1(PB).............(ii)\dfrac{x\cos \alpha }{a}+\dfrac{y\sin \alpha }{b}=1\left( PB \right).............\left( ii \right)
xcos⁡βa+ysin⁡βb=1(BQ).............(iii)\dfrac{x\cos \beta }{a}+\dfrac{y\sin \beta }{b}=1\left( BQ \right).............\left( iii \right)
Let us find intersecting point of equation (ii) and (iii);
By cross multiplication method from equation (ii) and (iii);
xsin⁡αb−sin⁡βb=−ycos⁡αa−cos⁡βa=−1cos⁡αasin⁡βb−sin⁡αcos⁡βab bx(sin⁡α−sin⁡β)=−aycos⁡α−cos⁡β=−abcos⁡αsin⁡β−sin⁡αcos⁡β \begin{aligned} & \dfrac{x}{\dfrac{\sin \alpha }{b}-\dfrac{\sin \beta }{b}}=\dfrac{-y}{\dfrac{\cos \alpha }{a}-\dfrac{\cos \beta }{a}}=\dfrac{-1}{\dfrac{\cos \alpha }{a}\dfrac{\sin \beta }{b}-\dfrac{\sin \alpha \cos \beta }{ab}} \\\ & \dfrac{bx}{\left( \sin \alpha -\sin \beta \right)}=\dfrac{-ay}{\cos \alpha -\cos \beta }=\dfrac{-ab}{\cos \alpha \sin \beta -\sin \alpha \cos \beta } \\\ \end{aligned}
Simplifying the above relation to get xx and yy
x=a(sin⁡α−sin⁡β)sin⁡αcos⁡β−cos⁡αsin⁡β,y=−b(cos⁡α−cos⁡β)sin⁡αcos⁡β−cos⁡αsin⁡βx=\dfrac{a\left( \sin \alpha -\sin \beta \right)}{\sin \alpha \cos \beta -\cos \alpha \sin \beta },y=\dfrac{-b\left( \cos \alpha -\cos \beta \right)}{\sin \alpha \cos \beta -\cos \alpha \sin \beta }
We have;
sin⁡C−sin⁡D=2sin⁡C−D2cos⁡C+D2 cos⁡C−cos⁡D=−2sin⁡C−D2sin⁡C+D2 sin⁡Ccos⁡D−cos⁡Csin⁡D=sin⁡(C−D) \begin{aligned} & \sin C-\sin D=2\sin \dfrac{C-D}{2}\cos \dfrac{C+D}{2} \\\ & \cos C-\cos D=-2\sin \dfrac{C-D}{2}\sin \dfrac{C+D}{2} \\\ & \sin C\cos D-\cos C\sin D=\sin \left( C-D \right) \\\ \end{aligned}
Therefore, we can rewrite xx and yyas;
x=2asin⁡(α−β2)cos⁡(α+β2)sin⁡(α−β),y=2bsin⁡α−β2sin⁡α+β2−sin⁡(α−β)x=\dfrac{2a\sin \left( \dfrac{\alpha -\beta }{2} \right)\cos \left( \dfrac{\alpha +\beta }{2} \right)}{\sin \left( \alpha -\beta \right)},y=\dfrac{2b\sin \dfrac{\alpha -\beta }{2}\sin \dfrac{\alpha +\beta }{2}}{-\sin \left( \alpha -\beta \right)}
We have;

& \sin 2\theta =2\sin \theta \cos \theta \\\ & x=\dfrac{2a\sin \left( \dfrac{\alpha -\beta }{2} \right)\cos \left( \dfrac{\alpha +\beta }{2} \right)}{2\sin \left( \dfrac{\alpha -\beta }{2} \right)\cos \left( \dfrac{\alpha -\beta }{2} \right)}=\dfrac{a\cos \left( \dfrac{\alpha +\beta }{2} \right)}{\cos \left( \dfrac{\alpha -\beta }{2} \right)} \\\ & y=\dfrac{2b\sin \left( \dfrac{\alpha -\beta }{2} \right)\sin \left( \dfrac{\alpha +\beta }{2} \right)}{2\sin \left( \dfrac{\alpha -\beta }{2} \right)\cos \left( \dfrac{\alpha -\beta }{2} \right)}=\dfrac{b\sin \left( \dfrac{\alpha +\beta }{2} \right)}{\cos \left( \dfrac{\alpha -\beta }{2} \right)} \\\ & \left( x,y \right)=\left( \dfrac{a\cos \left( \dfrac{\alpha +\beta }{2} \right)}{\cos \left( \dfrac{\alpha -\beta }{2} \right)},\dfrac{b\sin \left( \dfrac{\alpha +\beta }{2} \right)}{\cos \left( \dfrac{\alpha -\beta }{2} \right)} \right)..........\left( iv \right) \\\ \end{aligned}$$ Calculated $\left( x,y \right)$ in equation (iv) will lie on ${{x}^{2}}={{h}^{2}}$which is intersection of $PB$ and $BQ$ . Let us find out points $A$ or $C$ of which we need to find locus. Let us find out the intersection of $QC$ and $RC$ which is point $C$. Let's coordinate the point $C$ is $\left( {{x}_{_{1}}},{{y}_{1}} \right)$. The parametric coordinate of point $Q$ is $\left( a\cos \beta ,b\sin \beta \right)$. Now, by symmetry point $P$ and $R$ will lie exactly opposite to other as shown below; ![](https://www.vedantu.com/question-sets/af468323-01bf-4ddf-9f1b-d34353ea1ee21252562100661006269.png) Hence, parametric coordinate of point $R$is $a\cos \left( \pi +\alpha \right),b\sin \left( \pi +\alpha \right)\text{ or }-a\cos \alpha ,-b\sin \alpha .$ Now, let us write equation of tangents passing through $C$ i.e., $RC$ and $QC$ ; $\begin{aligned} & T=0 \\\ & \dfrac{-xa\cos \alpha }{{{a}^{2}}}\dfrac{-yb\sin \alpha }{{{b}^{2}}}=1 \\\ & \dfrac{x\cos \alpha }{a}+\dfrac{y\sin \alpha }{b}+1=0.............\left( v \right) \\\ \end{aligned}$ Another tangent through $Q$ is; $\dfrac{x\cos \beta }{a}+\dfrac{y\sin \beta }{b}-1=0.............\left( vi \right)$ Let us find out intersection of above two equations by cross multiplication method: $\begin{aligned} & \dfrac{x}{\dfrac{-\sin \alpha }{b}-\dfrac{\sin \beta }{b}}=\dfrac{-y}{\dfrac{-\cos \alpha }{a}-\dfrac{\cos \beta }{a}}=\dfrac{1}{\dfrac{\cos \alpha }{a}\dfrac{\sin \beta }{b}-\dfrac{\sin \alpha }{b}\dfrac{\cos \beta }{a}} \\\ & \dfrac{-bx}{\sin \alpha +\sin \beta }=\dfrac{ay}{\cos \alpha +\cos \beta }=\dfrac{ab}{\cos \alpha \sin \beta -\sin \alpha \cos \beta } \\\ \end{aligned}$ Now, we can write values of $x$ and $y$ as; $\begin{aligned} & x=\dfrac{a\left( \sin \alpha +\cos \beta \right)}{\sin \alpha \cos \beta -\cos \alpha \sin \beta } \\\ & y=\dfrac{b\left( \cos \alpha +\cos \beta \right)}{\cos \alpha \sin \beta -\sin \alpha \cos \beta } \\\ \end{aligned}$ We have, $\begin{aligned} & \sin C+\sin D=2\sin \dfrac{C+D}{2}\cos \dfrac{C-D}{2} \\\ & \cos C+\cos D=-2\cos \dfrac{C+D}{2}\cos \dfrac{C-D}{2} \\\ & \sin C\cos D-\cos C\sin D=\sin \left( C-D \right) \\\ \end{aligned}$ Therefore, we can write $x$ and $y$ as; $x=\dfrac{2a\sin \dfrac{\alpha +\beta }{2}\cos \dfrac{\alpha -\beta }{2}}{\sin \left( \alpha -\beta \right)}$ $\begin{aligned} & x=\dfrac{2a\sin \dfrac{\alpha +\beta }{2}\cos \dfrac{\alpha -\beta }{2}}{2\sin \dfrac{\alpha -\beta }{2}\cos \dfrac{\alpha -\beta }{2}} \\\ & x=\dfrac{a\sin \dfrac{\alpha +\beta }{2}}{\sin \dfrac{\alpha -\beta }{2}} \\\ \end{aligned}$ And, $\begin{aligned} & y=\dfrac{2b\cos \dfrac{\alpha +\beta }{2}\cos \dfrac{\alpha -\beta }{2}}{\sin \left( \beta -\alpha \right)} \\\ & y=\dfrac{2b\cos \dfrac{\alpha +\beta }{2}\cos \dfrac{\alpha -\beta }{2}}{-2\sin \dfrac{\alpha -\beta }{2}\cos \dfrac{\alpha -\beta }{2}} \\\ & y=\dfrac{-b\cos \dfrac{\alpha +\beta }{2}}{\sin \dfrac{\alpha -\beta }{2}} \\\ \end{aligned}$ Now, we have point $C\left( {{x}_{_{1}}},{{y}_{1}} \right)$as; $\left( {{x}_{_{1}}},{{y}_{1}} \right)=\left( \dfrac{a\sin \dfrac{\alpha +\beta }{2}}{\sin \dfrac{\alpha -\beta }{2}},\dfrac{-b\cos \dfrac{\alpha +\beta }{2}}{\sin \dfrac{\alpha -\beta }{2}} \right).............\left( vii \right)$ As we have point $B(x,y)$ calculated in equation (iv) and will satisfy equation ${{x}^{2}}={{h}^{2}}$. Putting value of $x$ from equation (iv) to ${{x}^{2}}={{h}^{2}}$, we get; $\dfrac{{{a}^{2}}{{\cos }^{2}}\dfrac{\alpha +\beta }{2}}{{{\cos }^{2}}\dfrac{\alpha -\beta }{2}}={{h}^{2}}...........\left( viii \right)$ Now, let us find out values of ${{\cos }^{2}}\dfrac{\alpha +\beta }{2}$,${{\cos }^{2}}\dfrac{\alpha -\beta }{2}$from equation (vii) in terms of ${{x}_{1}}\text{ and }{{y}_{1}}$, as; ${{x}_{_{1}}}=\dfrac{a\sin \dfrac{\alpha +\beta }{2}}{\sin \dfrac{\alpha -\beta }{2}},{{y}_{1}}=\dfrac{-b\cos \dfrac{\alpha +\beta }{2}}{\sin \dfrac{\alpha -\beta }{2}}$ Dividing ${{x}_{1}}\text{ and }{{y}_{1}}$, we get; $\left( \dfrac{{{x}_{1}}}{{{y}_{1}}} \right)=\dfrac{-a}{b}\tan \left( \dfrac{\alpha +\beta }{2} \right)$ Squaring both sides, we get; $$\left( \dfrac{{{x}_{1}}^{2}}{{{y}_{1}}^{2}} \right)=\dfrac{{{a}^{2}}}{{{b}^{2}}}{{\tan }^{2}}\left( \dfrac{\alpha +\beta }{2} \right)$$ We have relation $1+{{\tan }^{2}}\theta ={{\sec }^{2}}\theta $ or${{\tan }^{2}}\theta ={{\sec }^{2}}\theta -1,$using it in above equation, we get; $$\begin{aligned} & \dfrac{{{b}^{2}}{{x}_{1}}^{2}}{{{a}^{2}}{{y}_{1}}^{2}}={{\sec }^{2}}\dfrac{\alpha +\beta }{2}-1 \\\ & {{\sec }^{2}}\dfrac{\alpha +\beta }{2}=1+\dfrac{{{b}^{2}}{{x}_{1}}^{2}}{{{a}^{2}}{{y}_{1}}^{2}} \\\ & {{\sec }^{2}}\dfrac{\alpha +\beta }{2}=\dfrac{{{a}^{2}}{{y}_{1}}^{2}+{{b}^{2}}{{x}_{1}}^{2}}{{{a}^{2}}{{y}_{1}}^{2}} \\\ & Or\text{ co}{{\text{s}}^{2}}\dfrac{\alpha +\beta }{2}=\dfrac{{{a}^{2}}{{y}_{1}}^{2}}{{{a}^{2}}{{y}_{1}}^{2}+{{b}^{2}}{{x}_{1}}^{2}}............\left( ix \right) \\\ \end{aligned}$$ Now, let us calculate square of ${{x}_{1}}$; ${{x}_{_{1}}}^{2}=\dfrac{{{a}^{2}}{{\sin }^{2}}\dfrac{\alpha +\beta }{2}}{{{\sin }^{2}}\left( \dfrac{\alpha -\beta }{2} \right)}$ We have${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$; Hence; $\begin{aligned} & {{x}_{_{1}}}^{2}=\dfrac{{{a}^{2}}\left( 1-{{\cos }^{2}}\dfrac{\alpha +\beta }{2} \right)}{{{\sin }^{2}}\left( \dfrac{\alpha -\beta }{2} \right)} \\\ & {{\sin }^{2}}\dfrac{\alpha -\beta }{2}=\dfrac{{{a}^{2}}}{{{x}_{_{1}}}^{2}}\left( 1-\dfrac{{{a}^{2}}{{y}_{1}}^{2}}{{{a}^{2}}{{y}_{1}}^{2}+{{b}^{2}}{{x}_{1}}^{2}} \right) \\\ & {{\sin }^{2}}\dfrac{\alpha -\beta }{2}=\dfrac{{{a}^{2}}}{{{x}_{_{1}}}^{2}}\left( \dfrac{{{b}^{2}}{{x}_{1}}^{2}}{{{a}^{2}}{{y}_{1}}^{2}+{{b}^{2}}{{x}_{1}}^{2}} \right) \\\ & {{\sin }^{2}}\dfrac{\alpha -\beta }{2}=\dfrac{{{a}^{2}}{{b}^{2}}}{{{a}^{2}}{{y}_{1}}^{2}+{{b}^{2}}{{x}_{1}}^{2}} \\\ & Or\text{ }1-{{\cos }^{2}}\dfrac{\alpha -\beta }{2}=\dfrac{{{a}^{2}}{{b}^{2}}}{{{a}^{2}}{{y}_{1}}^{2}+{{b}^{2}}{{x}_{1}}^{2}} \\\ & {{\cos }^{2}}\dfrac{\alpha -\beta }{2}=\dfrac{{{a}^{2}}{{y}_{1}}^{2}+{{b}^{2}}{{x}_{1}}^{2}-{{a}^{2}}{{b}^{2}}}{{{a}^{2}}{{y}_{1}}^{2}+{{b}^{2}}{{x}_{1}}^{2}}...........\left( x \right) \\\ \end{aligned}$ Putting values of ${{\cos }^{2}}\dfrac{\alpha +\beta }{2},{{\cos }^{2}}\dfrac{\alpha -\beta }{2}$from equation (ix) and (x) in equation (viii), we get; $\begin{aligned} & \dfrac{{{a}^{2}}\left( \dfrac{{{a}^{2}}{{y}_{1}}^{2}}{{{a}^{2}}{{y}_{1}}^{2}+{{b}^{2}}{{x}_{1}}^{2}} \right)}{\left( \dfrac{{{a}^{2}}{{y}_{1}}^{2}+{{b}^{2}}{{x}_{1}}^{2}-{{a}^{2}}{{b}^{2}}}{{{a}^{2}}{{y}_{1}}^{2}+{{b}^{2}}{{x}_{1}}^{2}} \right)}={{h}^{2}} \\\ & \dfrac{{{a}^{4}}{{y}_{1}}^{2}}{{{a}^{2}}{{y}_{1}}^{2}+{{b}^{2}}{{x}_{1}}^{2}-{{a}^{2}}{{b}^{2}}}={{h}^{2}} \\\ & \dfrac{{{a}^{4}}{{y}_{1}}^{2}}{{{h}^{2}}}={{a}^{2}}{{y}_{1}}^{2}+{{b}^{2}}{{x}_{1}}^{2}-{{a}^{2}}{{b}^{2}} \\\ & {{a}^{2}}{{b}^{2}}={{y}_{1}}^{2}\left( {{a}^{2}}-\dfrac{{{a}^{2}}}{{{h}^{2}}} \right)+{{b}^{2}}{{x}_{1}}^{2} \\\ \end{aligned}$ Dividing both sides by ${{a}^{2}}{{b}^{2}}$, we get; $1=\dfrac{{{y}_{1}}^{2}}{{{b}^{2}}}\left( 1-\dfrac{{{a}^{2}}}{{{h}^{2}}} \right)+\dfrac{{{x}_{1}}^{2}}{{{a}^{2}}}$ Replacing $\left( {{x}_{1}},{{y}_{1}} \right)$ by $\left( x,y \right)$ to get the required locus, we get; $\dfrac{{{x}_{1}}^{2}}{{{a}^{2}}}+\dfrac{{{y}_{1}}^{2}}{{{b}^{2}}}\left( 1-\dfrac{{{a}^{2}}}{{{h}^{2}}} \right)=1$ Hence, proved. Note: One can calculate intersection of tangent $PA$ and $AS$ to get point $A$ where point $P\text{ and }S$ has parametric coordinates as $\left( a\cos \alpha ,b\sin \alpha \right),\left( a\cos \left( \pi +\beta \right),b\sin \left( \pi +\beta \right) \right)$. Solution will be the same. Calculation is the important part of these kinds of questions. One can use a substitution and elimination approach to find intersecting points of tangents but that will be a longer process than cross – multiplication which gives $\left( x,y \right)$ in one line. By symmetry of ellipse points $\left( P,R \right)\text{ and }\left( Q,S \right)$ will be opposite to each other at a difference of $180{}^\circ $ eccentric angle which is the key point of this question..