Question

A parallelepiped is formed by planes drawn through the point $P\left( 6,8,10 \right)$ and $Q\left( 3,4,8 \right)$ parallel to the coordinate planes. Find the length of edges and diagonals of parallelepiped.

Answer 1

To solve this question, first we will draw planes through the point $P\left( 6,8,10 \right)$ and $Q\left( 3,4,8 \right)$ parallel to the coordinate planes. Then, we observe that the parallelepiped formed is a cuboid so we will find length of edges by simply calculate the distances between planes and then calculate the length of diagonal by using the formula $\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}}$
Where,
$\begin{aligned} & l=\text{length} \\\ & \text{b=breadth} \\\ & \text{h=height} \\\ \end{aligned}$

Complete step-by-step answer:
We have given that a parallelepiped is formed by planes drawn through the point $P\left( 6,8,10 \right)$ and $Q\left( 3,4,8 \right)$ parallel to the coordinate planes.
Let us draw a parallelepiped through the point $P\left( 6,8,10 \right)$ and $Q\left( 3,4,8 \right)$ parallel to the coordinate planes.

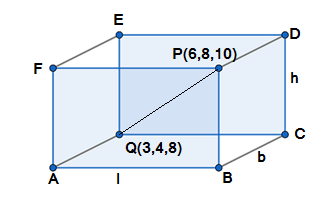
We get a cuboid, when we draw a diagram using given points.
We have to find the length of edges and diagonals of cuboid.
We have points $P\left( 6,8,10 \right)$ and $Q\left( 3,4,8 \right)$, let us assume
$\begin{aligned} & {{x}_{1}}=6;{{x}_{2}}=3 \\\ & {{y}_{1}}=8;{{y}_{2}}=4 \\\ & {{z}_{1}}=10;{{z}_{2}}=8 \\\ \end{aligned}$
Now, to find the length of edges we calculate the distance between planes.
Now, let us assume $\text{l=Length; b=breadth; h=height}$
So, we have
$\begin{aligned} & l={{y}_{1}}-{{y}_{2}} \\\ & l=8-4 \\\ & l=4 \\\ \end{aligned}$
$\begin{aligned} & b={{x}_{1}}-{{x}_{2}} \\\ & b=6-3 \\\ & b=3 \\\ \end{aligned}$
$\begin{aligned} & h={{z}_{1}}-{{z}_{2}} \\\ & h=10-8 \\\ & h=2 \\\ \end{aligned}$
Now, to calculate the length of diagonals we use the formula $\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}}$.
Now, substituting values we get
$\begin{aligned} & Diagonal=\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}} \\\ & Diagonal=\sqrt{{{4}^{2}}+{{3}^{2}}+{{2}^{2}}} \\\ & Diagonal=\sqrt{16+9+4} \\\ & Diagonal=\sqrt{29} \\\ & Diagonal=5.385 \\\ \end{aligned}$
So, the length of edges will be $4,3,2$ units and length of diagonal will be $5.385$ units.

Note: To solve such types of questions the key concept is to draw a diagram. It is important to draw a diagram using the points given in the question, so we get a clear idea about the shape. If we don’t draw a diagram, we are not sure about what shape is formed and we are not able to find the length of edges and diagonals.