Question
Question: A parallelepiped is formed by planes drawn through the points \(P(6,8,10)\) and \(Q(3,4,8)\) paralle...
A parallelepiped is formed by planes drawn through the points P(6,8,10) and Q(3,4,8) parallel to the coordinate planes. Find the length of edges and diagonals of the parallelepiped.
Solution
Hint : For solving this question first we will draw planes through the points P(6,8,10) and Q(3,4,8) parallel to the coordinate planes. After that, we will prove that parallelepiped formed by the given planes will be a cuboid and we will find its dimensions. Moreover, we will use the formula l2+b2+h2 to find the body diagonal of the cuboid of length l , breadth b and height h .
Complete step by step solution :
Given:
We have to find the length of edges and diagonals of the parallelepiped formed by planes drawn through the points P(6,8,10) and Q(3,4,8) parallel to the coordinate planes.
Now, before we proceed we should know that if there is a point A(x1,y2,z2) then x=x1 , y=y1 and z=z1 planes will pass through point A(x1,y2,z2) and parallel to the coordinate planes.
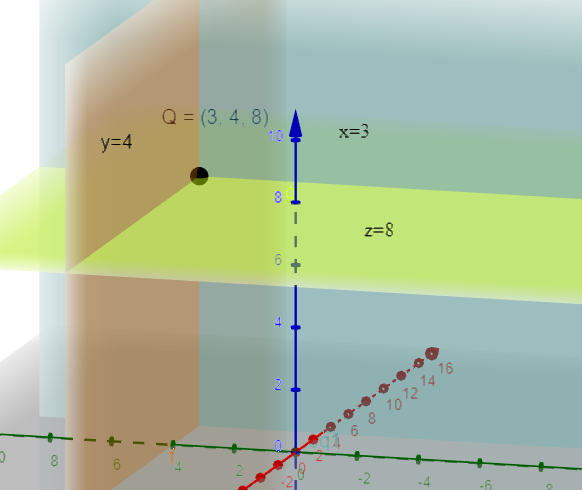
Now, from the above discussion, we conclude that, x=6 , y=8 and z=10 planes will be passing through point P(6,8,10) and parallel to the coordinate planes. For more clarity look at the figure given below:

Now, from the above discussion, we conclude that, x=3 , y=4 and z=8 planes will be passing through point Q(3,4,8) and parallel to the coordinate planes. For more clarity look at the figure given below:
Now, there are the following six planes:
x=6 and x=3y=8 and y=4z=10 and z=8
Now, parallelepiped formed by the above six planes will be a cuboid. For more clarity look at the figure given below:
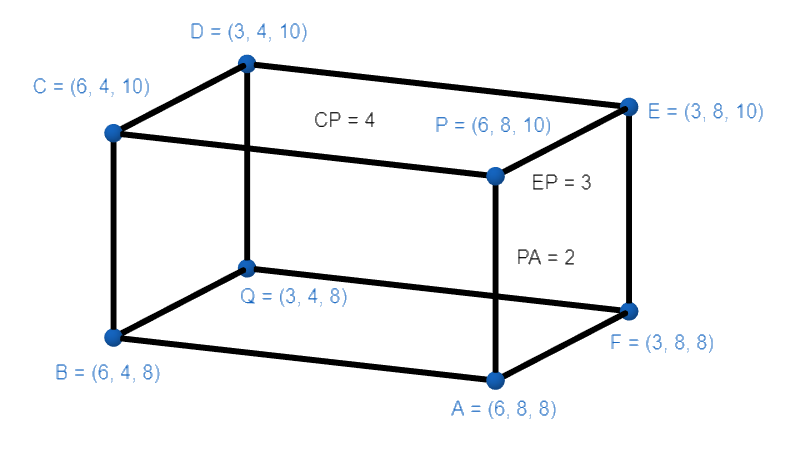
Now, to find the dimensions of the cuboid we will find the distance between the following planes:
x=6 and x=3y=8 and y=4z=10 and z=8
Now, as the above three pairs of planes are parallel so, we will simply find the difference in their values.
For length find the distance between planes y=8 and y=4 , for breadth find the distance between planes x=6 and x=3 , and for height find the distance between planes z=10 and z=8 Then,
Length=l=8−4=4Breadth=b=6−3=3Height=h=10−8=2
Now, from the above result, we conclude that the length, breadth and height of the cuboid will be 4, 3 and 2 units respectively.
Now, as we know that length of the body diagonal of the cuboid of length l , breadth b and height h is l2+b2+h2 . Then,
Length of the body diagonal =l2+b2+h2=42+32+22=16+9+4=29 units.
Now, we conclude that the required parallelepiped will be a cuboid of length, breadth and height of the cuboid will be 4, 3 and 2 units respectively and length of the diagonal of the parallelepiped will be 29≈5.385 units.
Note : The coordinates of the vertices of the parallelepiped can be found out by finding the point of intersection of the planes taken 3 at a time. For example, the point of intersection of the planes x=6, y=8 and z=10 is (6,8,10), which is the coordinate of the vertex P.
