Question
Question: A parallel plate capacitor with square plates is filled with four dielectrics of dielectric constant...
A parallel plate capacitor with square plates is filled with four dielectrics of dielectric constants K1,K2,K3,K4 arranged as shown in the figure. The effective dielectric constant K will be:
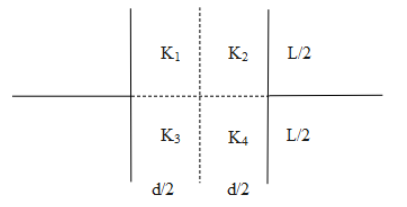
A. K=2(K1+K2+K3+K4)(K1+K2)(K3+K4)
B.K=K1+K2+K3+K4(K1+K2)(K3+K4)
C.K=2(K1+K2+K3+K4)(K1+K4)(K2+K3)
D. K=K1+K2+K3+K4(K1+K3)(K2+K4)
Solution
A capacitor is an energy storage device in which the energy is stored in the form of an electric field. In absence of any external energy source, a charged capacitor can serve as an energy source. The dielectric is the insulating (non-conducting) material which is present between the two conducting plates of the area A and parted by each other by a distance d.
Complete answer:
The value of capacitance of a capacitor is given as the:
C=dKAε0
Here the area and distance between the two plates will be divided into two equal sections. As per the arrangement of the dielectric of different K values in a capacitor, we can dissect this capacitor in four different capacitors which are arranged as per the diagram shown below,
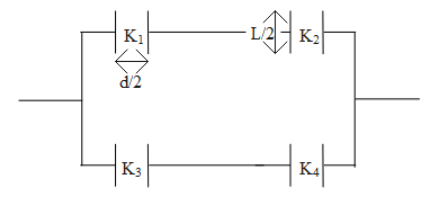
So the value of capacitance of each section of the capacitor will be given as,
C′=2dKx2Aε0⇒C′=dKxAε0
So when the capacitors are connected in series the total capacitance is given as,
C1=C11+C21
As the capacitor of dielectric constant K1&K2 are connected in serial the sum of their capacitance will be,
C1=K1Aε0d+K2Aε0d⇒Ca=dAε0(K1+K2K1K2)......(1)
Similarly, the sum of the capacitance of dielectric constant K3&K4 will be given as,
⇒Cb=dAε0(K3+K4K3K4)......(2)
When the two capacitors are connected in series the sum of capacitance is given as,
C=C1+C2+...
SO from equation (1) and (2) the total capacitance of the capacitor will be,
C=Ca+Cb⇒dKAε0=dAε0(K1+K2K1K2+K3+K4K3K4)
So by simplifying the above equation the value of the dielectric constant of the capacitor is given as,
K=K1+K2K1K2+K3+K4K3K4∴K=2(K1+K2+K3+K4)(K1+K2)(K3+K4) $$
Thus, when we give a glance over the options we found that the correct option which satisfies the question is Option A.
Note:
The capacitors can only charge when an AC source is connected across it. It short circuits the circuit in the presence of a direct current. In most of the complex circuits where we don’t want DC output, the capacitors are used as a barrier for the DC current and allow only the AC current to pass through it.
