Solveeit Logo
Login

Question

Question: A parallel plate capacitor with circular plates and a capacitance C has the radius of each plate dou...

A parallel plate capacitor with circular plates and a capacitance C has the radius of each plate doubled, and the distance between the plates doubled. What is the new capacitance?

A. C2\dfrac{C}{2}
B. CC
C. 2C2C
D. 4C4C

Explanation

Solution

In this question, it is said that the radius and the distance between the plates are doubled for a capacitor so first, we will find the initial capacitance for circular plates and then we will compare this with the capacitance of the new capacitor.

Complete step by step answer:
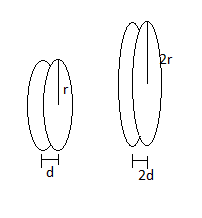
The initial distance between the plates =d = d
Initial radius of each plate=r = r
So the area of the circular plate will be A=πr2A = \pi {r^2}
Now as we know that the capacitance for a parallel plate capacitance is given by the formulaC=∈0Ad−−(i)C = \dfrac{{{ \in _0}A}}{d} - - (i)
So we can write the capacitance for parallel circular plates as
C=∈0(πr2)d−−(ii)C = \dfrac{{{ \in _0}\left( {\pi {r^2}} \right)}}{d} - - (ii)
Now it is said that that radius of each plate is doubled and also the distance between the plates doubled, so the
The new radius of the circular plate for the capacitor is r′=2rr' = 2r
New distance between the plates =d′=2d = d' = 2d
So the area of the parallel circular plates becomeA′=π(2r)2=4πr2=4AA' = \pi {\left( {2r} \right)^2} = 4\pi {r^2} = 4A
Hence the capacitance for the new circular plates become

C′=∈0A′d′ =∈04A2d =2∈0Ad  C' = \dfrac{{{ \in _0}A'}}{{d'}} \\\ = \dfrac{{{ \in _0}4A}}{{2d}} \\\ = 2\dfrac{{{ \in _0}A}}{d} \\\

Now since C=∈0AdC = \dfrac{{{ \in _0}A}}{d}from equation (i), hence we can write
C′=2CC' = 2C
Hence we can say the capacitance becomes doubled.

So, the correct answer is “Option C”.

Note:
Students must know that the capacitance for parallel plate capacitors is directly proportional to the area of the plates so capacitance will vary directly with the increase or decrease in the area of the plates. Capacitance for a parallel plate capacitance is given by the formula C=∈0AdC = \dfrac{{{ \in _0}A}}{d}, where A is the area of the parallel plate, d is the distance between the parallel plates and ∈0{ \in _0} is the permittivity of the free space.