Question

A parallel plate capacitor with air between the plates has capacitance of $9\,pF$.The separation between plates is ‘$d$’. The space between the plates is now filled with two dielectrics. One of the dielectrics has dielectric constant ${{k}_{1}}=3$ and thickness $\dfrac{d}{3}$ while the other one has dielectric constant ${{k}_{2}}=6$ and thickness $\dfrac{2d}{3}$. Capacitance of the capacitor is now:
A. $1.8\,pF$
B. $45\,pF$
C. $40.5\,pF$
D. $20.25\,pF$

Answer 1

In order to solve the given problem we will first see the definitions of capacitor, capacitance and dielectrics and then by using the formula for capacitance we will find the capacitance of the new formed capacitor.

Formula used:
$C=\dfrac{A{{\varepsilon }_{0}}}{d}$
Where, $C$ is the capacitance, $A$ is the area of plates of capacitor, ${{\varepsilon }_{0}}$ is the permittivity of free space and $d$ is the distance between two parallel plates of capacitor.

Complete step by step answer:
Let us see the definitions first: Two parallel plates when connected across a battery, the plates are charged and an electric field is created between them, this setup is known as the parallel plate capacitor. The ability of a substance to store an electric charge is known as capacitance of that substance. The property of transferring of electric force without conduction is known as dielectric of a substance (insulator). Below is the reference diagram of the capacitor,

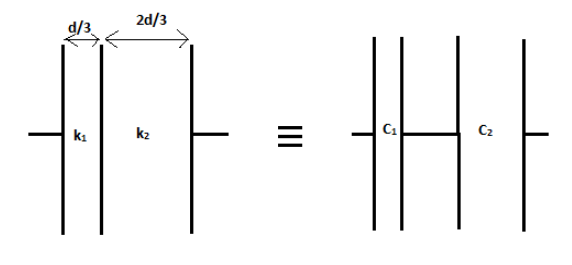
For the air filled capacitor, we know that, $C=\dfrac{A{{\varepsilon }_{0}}}{d}=9\,pF$
As per the data provided in the question there are two capacitors with capacitances ${{C}_{1}}$ and ${{C}_{2}}$ and they are connected in series.
${{C}_{1}}=\dfrac{A{{k}_{1}}{{\varepsilon }_{0}}}{\left( d/3 \right)} \\\ \Rightarrow {{C}_{1}} =9\dfrac{A{{\varepsilon }_{0}}}{d} \\\ \Rightarrow {{C}_{1}}=9C$ as ${{k}_{1}}=3$
$\Rightarrow {{C}_{2}}=\dfrac{A{{k}_{2}}{{\varepsilon }_{0}}}{\left( 2d/3 \right)} \\\ \Rightarrow {{C}_{2}} =9\dfrac{A{{\varepsilon }_{0}}}{d} \\\ \Rightarrow {{C}_{2}} =9C$ as ${{k}_{2}}=6$
The equivalent capacitance,
${{C}_{eq}}=\dfrac{{{C}_{1}}{{C}_{2}}}{{{C}_{1}}+{{C}_{2}}} \\\ \Rightarrow {{C}_{eq}} =\dfrac{\left( 9C \right)\left( 9C \right)}{9C+9C} \\\ \Rightarrow {{C}_{eq}} =\dfrac{9}{2}C \\\ \Rightarrow {{C}_{eq}} =\left( \dfrac{9}{2} \right)9 \\\ \therefore {{C}_{eq}}=40.5pF$

Hence, the equivalent capacitance is 40.5 pF.

Note: One must remember the formula of capacitance in order to solve the above question. One must note that the equivalent capacitor depends upon whether the capacitors are connected in series or in parallel to each other, if the capacitor were connected in parallel then the equivalent capacitor shall change.