Question

A parallel plate capacitor of capacitance C has spacing d between two plates having area A.
The region between the plates is filled with N dielectric layers, parallel to its plates, each with N dielectric layers, parallel to its plates, each with thickness ${{\delta = }}\dfrac{{{d}}}{{{N}}}$. The dielectric constant of the ${{{m}}^{{{th}}}}$s layer is ${{{K}}_{{m}}} = {{K}}\left( {{{1 + }}\dfrac{{{m}}}{{{N}}}} \right)$. For a very large N$\left( { > {{10}^3}} \right)$, the capacitance C is${{\alpha }}\left( {\dfrac{{{{K}}{{{\varepsilon }}_{{0}}}{{A}}}}{{{{dln2}}}}} \right)$.
The value of $\alpha$will be ……………………………. [${{{\varepsilon }}_{{0}}}$is the permittivity of free space]

Answer 1

To find the required value for α we have to understand the region between the plates having N dielectric layers is equivalent to combination N-capacitors having different values of dielectric constant. So, we have to calculate the small elemental capacitance for each capacitor in a sequent manner and then take their equivalent capacitance. We take the formula for an elemental capacitor as:- ${{dc = }}\dfrac{{{{{\varepsilon }}_{{0}}}{{{K}}_{{m}}}{{A}}}}{{{{dx}}}}$ , where ${{dc }}$is the elemental capacitance dx is the spacing between plates having elemental area A. Then after we will calculate the equivalent capacitance by the formula: $\dfrac{1}{{{{{C}}_{{{eq}}}}}} = \int {\dfrac{1}{{{{dc}}}}}$ and get the required value for α.

Complete step by step answer:
To calculate the elemental capacitance we are taking small elemental capacitor at a distance x of dielectric thickness dx along with the spacing of the plate as shown in figure 1.1
Formula used: ${{dc = }}\dfrac{{{{{\varepsilon }}_{{0}}}{{{K}}_{{m}}}{{A}}}}{{{{dx}}}}$, where ${{dc }}$is the elemental capacitance dx is the spacing between plates having elemental area A.

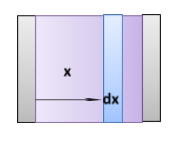
As per the information given in the question we have given that-

${{\delta = }}\dfrac{{{d}}}{{{N}}}$……………. (i)
${{{K}}_{{m}}} = {{K}}\left( {{{1 + }}\dfrac{{{m}}}{{{N}}}} \right)$………. (ii)
${{C = \alpha }}\left( {\dfrac{{{{K}}{{{\varepsilon }}_{{0}}}{{A}}}}{{{{dln2}}}}} \right)$………….(iii)

$\Rightarrow \dfrac{x}{m} = \dfrac{d}{N}$……………… (iv)
For the series combination of dielectrics formula used:
$\dfrac{1}{{{{{C}}_{{{eq}}}}}} = \int {\dfrac{1}{{{{dc}}}}}$………………… (v)
Since, $\dfrac{{{1}}}{{{{dc}}}}{{ = }}\dfrac{{{{dx}}}}{{{{{k}}_{{m}}}{{{\varepsilon }}_{{0}}}{{A}}}}$
$\Rightarrow \dfrac{{{1}}}{{{{dc}}}}{{ = }}\dfrac{{{{dx}}}}{{{{{k}}_{{m}}}{{{\varepsilon }}_{{0}}}{{A}}}}$…………… (vi)
Substitute the value of $\dfrac{1}{{{{dc}}}}$in the equation (v), we get
$\dfrac{{{1}}}{{{{{C}}_{{{eq}}}}}}{{ = }}\int\limits_0^d {\dfrac{{{{dx}}}}{{{{{K}}_{{m}}}{{{\varepsilon }}_{{0}}}{{A}}}}}$…………….. (vii)
Using the equation (iii) in equation (vii)
$\Rightarrow \dfrac{{{1}}}{{{{{C}}_{{{eq}}}}}}{{ = }}\int\limits_{{0}}^{{d}} {\dfrac{{{{dx}}}}{{{{K}}{{{\varepsilon }}_{{0}}}{{A}}\left( {{{1 + }}\dfrac{{{m}}}{{{N}}}} \right)}}}$
$\Rightarrow \dfrac{{{1}}}{{{{{C}}_{{{eq}}}}}}{{ = }}\int\limits_{{0}}^{{d}} {\dfrac{{{{dx}}}}{{{{K}}{{{\varepsilon }}_{{0}}}{{A}}\left( {{{1 + }}\dfrac{x}{d}} \right)}}}$
$\Rightarrow \dfrac{{{1}}}{{{{{C}}_{{{eq}}}}}}{{ = }}\int\limits_{{0}}^{{d}} {\dfrac{{{{ddx}}}}{{{{K}}{{{\varepsilon }}_{{0}}}{{A}}\left( {{{d + x}}} \right)}}}$

$\Rightarrow \dfrac{{{1}}}{{{{{C}}_{{{eq}}}}}}{{ = }}\dfrac{{{d}}}{{{{K}}{{{\varepsilon }}_{{0}}}{{A}}}}\ln 2$
$\Rightarrow {{{C}}_{{{eq}}}}{{ = }}\dfrac{{{{K}}{{{\varepsilon }}_{{0}}}{{A}}}}{{{{d}}\ln 2}}$……………….. (viii)
On comparing both the equation (viii) and (ii), we get
$\alpha = 1$

$\therefore$ The value of $\alpha = 1$

Note:
In order to answer this type of question, the key is to know the basic algorithm behind the calculation of equivalent capacitance of a system having dielectric varies with certain parameters like varies with distance, varies with filling orientation, etc. So for grasping the ideas behind such conceptual problems one should have to practice a lot of numerical and derivative type problems on this topic.